Advertisements
Advertisements
प्रश्न
A line intersects x-axis at point (−2, 0) and cuts off an intercept of 3 units from the positive side of y-axis. Find the equation of the line.
उत्तर
Let line intersects x-axis at P(−2, 0) and cuts off an intercept of 3 units at Q.
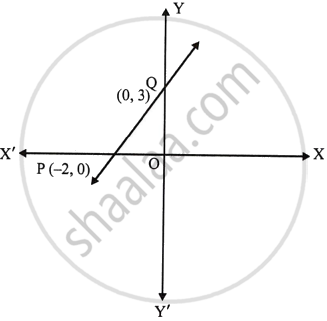
∴ Co-ordinates of Q are (0, 3)
Now, slope of line PQ
`m = (y_2 - y_1)/(x_2 - x_1)`
= `(0 - 3)/(-2 - 0)`
= `(-3)/(-2)`
= `3/2`
∴ Equation of line PQ will be
y − y1 = m(x − x1)
`=> y - 3 = 3/2 (x - 0)`
`=> y - 3 = 3/2 x`
`=>` 2y – 6 = 3x
`=>` 2y = 3x + 6
Hence, required equation of line is 2y = 3x + 6
APPEARS IN
संबंधित प्रश्न
Solve the following inequation and represent the solution set on a number line.
`-8 1/2 < -1/2 -4x <= 7 1/2`, x ∈ 1
A(2, 5), B(–1, 2) and C(5, 8) are the vertices of a triangle ABC, `M' is a point on AB such that AM: MB = 1: 2. Find the coordinates of 'M'. Hence find the equation of the line passing through the points C and M
The line `(3x)/5 - (2y)/3 + 1 = 0` contains the point (m, 2m – 1); calculate the value of m.
Find the point of intersection of the lines 4x + 3y = 1 and 3x − y + 9 = 0. If this point lies on the line (2k – 1) x – 2y = 4; find the value of k.
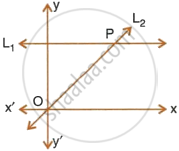
Given equation of line L1 is y = 4.
- Write the slope of line L2 if L2 is the bisector of angle O.
- Write the co-ordinates of point P.
- Find the equation of L2.
The line y = 6- `(3"x")/2` passes through the point (r,3). Find the value of r.
Find the inclination of a line whose gradient is 5.6713
Find the equation of a line passing through (8,3) and making an angle of 45° with the positive direction of the y-axis.
Find the equation of a line that has Y-intercept 3 units and is perpendicular to the line joining (2, – 3) and (4, 2).
Find the equation of a line parallel to 2y = 6x + 7 and passing through (–1, 1).
