Advertisements
Advertisements
प्रश्न
Find the point of intersection of the lines 4x + 3y = 1 and 3x − y + 9 = 0. If this point lies on the line (2k – 1) x – 2y = 4; find the value of k.
उत्तर
Given lines are;
4x + 3y = 1 ...(i)
3x – y = –9 ...(ii)
Multiplying (i) by 1 and (ii) 3; we have
4x + 3y = 1
9x – 3y = –27
On Adding, we get :
13x = –26
`\implies x = -26/13 = -2`
From (ii), we have
3x – y = –9
`\implies` 3(–2) – y = –9
`\implies` −6 – y = –9
`\implies` –y = –9 + 6 = –3
∴ y = 3
∴ The point of intersection is (–2, 3)
∴ The line (2k – 1) x – 2y = 4 passes through that point (–2, 3).
∴ The point (–2, 3) satisfy it.
∴ (2k – 1)(–2) – 2(3) = 4
`\implies` −4k + 2 – 6 = 4
`\implies` −4k – 4 = 4
`\implies` −4k = 4 + 4 = 8
∴ `k = 8/(-4) = -2`
Hence point of intersection is (–2, 3) and value of k = –2
APPEARS IN
संबंधित प्रश्न
State, true or false :
The point (–3, 0) lies on the line x + 3 = 0
The line through P (5, 3) intersects y-axis at Q.
write the equation of the line
The line segment joining the points A(3, −4) and B(−2, 1) is divided in the ratio 1 : 3 at point P in it. Find the co-ordinates of P. Also, find the equation of the line through P and perpendicular to the line 5x – 3y = 4.
A line 5x + 3y + 15 = 0 meets y-axis at point P. Find the co-ordinates of points P. Find the equation of a line through P and perpendicular to x – 3y + 4 = 0.
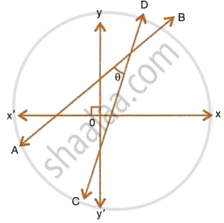
The given figure (not drawn to scale) shows two straight lines AB and CD. If equation of the line AB is : y = x + 1 and equation of line CD is : y = `sqrt(3)x - 1`. Write down the inclination of lines AB and CD; also, find the angle θ between AB and CD.
Find the value of p if the line 3y = 5x - 7 passes through the point (p,6).
Find the equation of a line whose slope and y-intercept are m = 2, c = -5
X(4,9), Y(-5,4) and Z(7,-4) are the vertices of a triangle. Find the equation of the altitude of the triangle through X.
Find the equation of a line which is inclined to x axis at an angle of 60° and its y – intercept = 2.
Find the equation of a line with slope 1 and cutting off an intercept of 5 units on Y-axis.
