Advertisements
Advertisements
प्रश्न
The vertices of a triangle are A(10, 4), B(- 4, 9) and C(- 2, -1). Find the
उत्तर
Let AD, BE and CF be the three altitudes of ΔABC then
AD ⊥ BC
BE ⊥ CA
and CF ⊥ AB.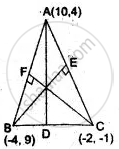
Slope of BC = `(-1 - 9)/(-2 + 4)` = -5
Since AD ⊥ BC
Slope of BC x slope of AD = -1
Slope of AD = `(-1)/(-5) = (1)/(5)`
Therefore AD ⊥ BC
Since, AD passes through A(10, 4)
So, equation of AD is
y - y1 = m (x - x1)
y - 4 = `(1)/(5) (x - 10)`
⇒ 5y - 20 = x - 10
⇒ x - 5y + 10 = 0 ...(i)
Now , Slope of AC = `(4 + 1)/(10 + 2) = (-5)/(12)`
since BE ⊥ AC
Slope of BE x Slope of AC = -1
So, Slope of BE = `(-1 xx 12)/(5) = -(12)/(5)`.
Equation of BE which passes through B(-4, 9) is
y - y1 = m(x - x1)
y - 9 = `(-12)/(5)(x + 4)`
or 12x + 5y + 3 = 0 ...(ii)
Slope of AB x Slope of CF = -1
⇒ `-(5)/(14)` x Slope of CF = -1
⇒ Slope of CF = `(14)/(5)`
Equation of CF which passes through C(-2, -1) is
y - y1 = m (x - x1)
y + 1 = `(14)/(5) (x + 2)`
⇒ 14x - 5y + 23 = 0 ...(iii)
Thus, the equation of altitudes of ΔABC are
x - 5y + 10 = 0
12x + 5y + 3 = 0
and 14x - 5y + 23 = 0.
APPEARS IN
संबंधित प्रश्न
Find the slope of the line perpendicular to AB if : A = (0, −5) and B = (−2, 4)
Without using the distance formula, show that the points A(4, 5), B(1, 2), C(4, 3) and D(7, 6) are the vertices of a parallelogram.
Find the slope and the inclination of the line AB if : A = `(0, - sqrt(3))` and B = (3, 0)
The line through A(−2, 3) and B(4, b) is perpendicular to the line 2x – 4y = 5. Find the value of b.
Angles made by the line with the positive direction of X–axis is given. Find the slope of these line.
60°
Find the slope of a line, correct of two decimals, whose inclination is 45°
Find the slope and the y-intercept of the following line 3x + y = 7
Find the slope and the y-intercept of the following line 2x + 3y = 12
Find the Slope of the line having inclination 45°.
Given that (a, 2a) lies on line`(y)/(2) = 3 - 6`.Find the value of a.
