Advertisements
Advertisements
प्रश्न
The vertices of a triangle are A(10, 4), B(- 4, 9) and C(- 2, -1). Find the
उत्तर
Let AD, BE and CF be the three altitudes of ΔABC then
AD ⊥ BC
BE ⊥ CA
and CF ⊥ AB.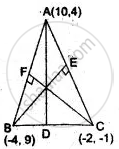
Slope of BC = `(-1 - 9)/(-2 + 4)` = -5
Since AD ⊥ BC
Slope of BC x slope of AD = -1
Slope of AD = `(-1)/(-5) = (1)/(5)`
Therefore AD ⊥ BC
Since, AD passes through A(10, 4)
So, equation of AD is
y - y1 = m (x - x1)
y - 4 = `(1)/(5) (x - 10)`
⇒ 5y - 20 = x - 10
⇒ x - 5y + 10 = 0 ...(i)
Now , Slope of AC = `(4 + 1)/(10 + 2) = (-5)/(12)`
since BE ⊥ AC
Slope of BE x Slope of AC = -1
So, Slope of BE = `(-1 xx 12)/(5) = -(12)/(5)`.
Equation of BE which passes through B(-4, 9) is
y - y1 = m(x - x1)
y - 9 = `(-12)/(5)(x + 4)`
or 12x + 5y + 3 = 0 ...(ii)
Slope of AB x Slope of CF = -1
⇒ `-(5)/(14)` x Slope of CF = -1
⇒ Slope of CF = `(14)/(5)`
Equation of CF which passes through C(-2, -1) is
y - y1 = m (x - x1)
y + 1 = `(14)/(5) (x + 2)`
⇒ 14x - 5y + 23 = 0 ...(iii)
Thus, the equation of altitudes of ΔABC are
x - 5y + 10 = 0
12x + 5y + 3 = 0
and 14x - 5y + 23 = 0.
APPEARS IN
संबंधित प्रश्न
Find the slope of the line passing through the points A(2, 3) and B(4, 7).
The line through A(–2, 3) and B(4, b) is perpendicular to the line 2x – 4y = 5. Find the value of b.
Find the value(s) of k so that PQ will be parallel to RS. Given : P(3, −1), Q(7, 11), R(−1, −1) and S(1, k)
The line through A(−2, 3) and B(4, b) is perpendicular to the line 2x – 4y = 5. Find the value of b.
Angles made by the line with the positive direction of X–axis is given. Find the slope of these line.
90°
Show that the line joining the points A(4, 8) and B(5, 5) is parallel to the line joining the points C(2, 4) and D(1, 7).
Find the slope of a line passing through the given pair of points (3,7) and (5,13)
Find the slope of a line parallel to the given line 4x-2y = 3
Find the slope and the y-intercept of the following line x - 2 = `(5 - 3"y")/2`
Find slope of a line passing through the points A(3, 1) and B(5, 3).
