Advertisements
Advertisements
प्रश्न
A(7, −1), B(4, 1) and C(−3, 4) are the vertices of a triangle ABC. Find the equation of a line through the vertex B and the point P in AC; such that AP : CP = 2 : 3.
उत्तर
P divides AC in the ratio of 2 : 3
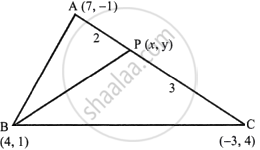
∴ Co-ordinates of P will be
`((m_1x_2 + m_2x_1)/(m_1 + m_2),(m_1y_2 + m_2y_1)/(m_1 + m_2))`
`((2(-3) + 3(7))/(2 + 3),(2 xx 4 + 3 xx (-1))/(2 + 3))`
= `((-6 + 21)/5, (8 - 3)/5)`
= `(15/5, 5/5)`
= (3, 1)
∴ Slope of line passing through B and P
= `(y_2 - y_1)/(x_2 - x_1)`
= `(1 - 1)/(3 - 4)`
= `0/(-1)`
= 0
∴ Equation of the required line is given by y – y1 = m(x – x1)
`=>` y – 1 = 0(x – 4)
`=>` y – 1 = 0
`=>` y = 1
APPEARS IN
संबंधित प्रश्न
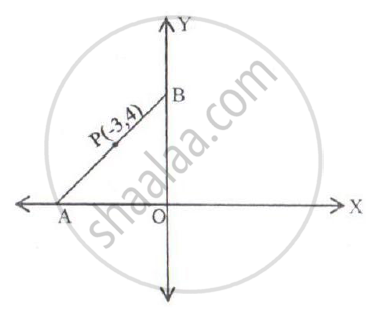
In the figure given below, the line segment AB meets X-axis at A and Y-axis at B. The point P(-3, 4) on AB divides it in the ratio 2:3. Find the coordinates of A and B.
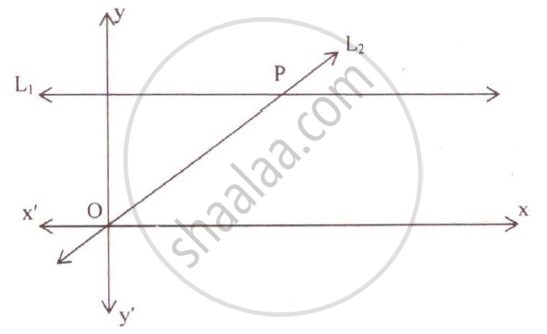
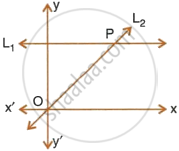
Given the equation of line L, is y = 4.
(1) Write the slope of line L2, if L2, is the bisector of angle O.
(2) Write the co–ordinates of point P.
(3) Find the equation of L2.
Find the equation of a line which passes through (5, 4) and makes an angle of 60° with the positive direction of the x-axis.
Find the equation of a line passing through the point (2, 3) and having the x-intercept of 4 units.
The given figure (not drawn to scale) shows two straight lines AB and CD. If equation of the line AB is : y = x + 1 and equation of line CD is : y = `sqrt(3)x - 1`. Write down the inclination of lines AB and CD; also, find the angle θ between AB and CD.
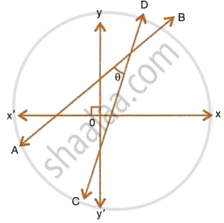
Given equation of line L1 is y = 4.
- Write the slope of line L2 if L2 is the bisector of angle O.
- Write the co-ordinates of point P.
- Find the equation of L2.
The line 4x + 3y = 11 bisects the join of ( 6,m) and (p,9). Find the value of m.
Find the value of a line parallel to the following line:
`(2"x")/5 + "y"/3` = 2
Find the equation of a line passing through the intersection of x + 2y + 1= 0 and 2x - 3y = 12 and perpendicular to the line 2x + 3y = 9
PQ is straight line of 13 units. If P has coordinate (2, 5) and Q has coordinate (x, – 7) find the possible values of x.
