Advertisements
Advertisements
प्रश्न
The line x – 6y + 11 = 0 bisects the join of (8, −1) and (0, k). Find the value of k.
उत्तर
The given line bisects the join of A(8, −1) and B(0, k), so the co-ordinates of the mid-point of AB will satisfy the equation of the line.
The co-ordinates of the mid-point of AB are
`((8 + 0)/2, (-1 + k)/2) = (4(-1 + k)/2)`
Substituting x = 4 and `y = (-1 + k)/2` in the given equation, we have:
x − 6y + 11 = 0
`4 - 6((-1 + k)/2) + 11 = 0`
`6((-1 + k)/2) = 15`
`(-1 + k)/2 = 15/6`
`(-1 + k)/2 = 5/2`
−1 + k = 5
k = 6
APPEARS IN
संबंधित प्रश्न
Solve the following inequation and represent the solution set on the number line 2x – 5 <= 5x + 4 < 11, where x ∈ I
Find the equation of the line whose slope is `-5/6` and x-intercept is 6.
A line 5x + 3y + 15 = 0 meets y-axis at point P. Find the co-ordinates of points P. Find the equation of a line through P and perpendicular to x – 3y + 4 = 0.
A line intersects x-axis at point (−2, 0) and cuts off an intercept of 3 units from the positive side of y-axis. Find the equation of the line.
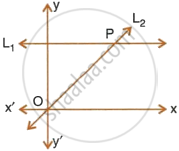
Given equation of line L1 is y = 4.
- Write the slope of line L2 if L2 is the bisector of angle O.
- Write the co-ordinates of point P.
- Find the equation of L2.
Find if the following points lie on the given line or not:
(7, -2) on the line 5x + 7y = 11
The line 7x - 8y = 4 divides join of (-8,-4) and (6,k) in the ratio of 2 : 5. Find the value of k.
P is a point on the line segment AB dividing it in the ratio 2 : 3. If the coordinates of A and Bare (-2,3) and (8,8), find if Plies on the line 7x - 2y =4.
Find the equation of a line passing through (2,5) and making and angle of 30° with the positive direction of the x-axis.
Find the equation of a line passing through (3, – 2) and perpendicular to the line.
x - 3y + 5 = 0.
