Advertisements
Advertisements
प्रश्न
Find the equation of a straight line which cuts an intercept – 2 units from Y-axis and being equally inclined to the axis.
उत्तर
Since, the required line is equally inclined with coordinate axis, therefore, it makes either an angle of 45° or 135° with the X-axis.
So, its slope is m = tan 45° ⇒ m = 1
or m = tan 135° ⇒ m = -1
Y-intercept, c = -2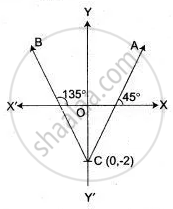
Hence, the equation of required lines are
y = mx + x
i.e., y = 1·x - 2 or y = -1·x - 2
⇒ y = x - 2 or y = -x - 2
⇒ x - y - 2 = 0 or x + y + 2 = 0.
APPEARS IN
संबंधित प्रश्न
A(2, 5), B(–1, 2) and C(5, 8) are the vertices of a triangle ABC, `M' is a point on AB such that AM: MB = 1: 2. Find the coordinates of 'M'. Hence find the equation of the line passing through the points C and M
Find, which of the following points lie on the line x – 2y + 5 = 0 :
(2, –1.5)
The point (−3, 2) lies on the line ax + 3y + 6 = 0, calculate the value of a.
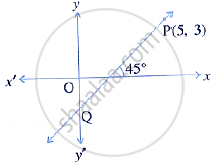
The line through P (5, 3) intersects y-axis at Q.
Find the co-ordinates of Q.
Find if the following points lie on the given line or not:
(-1, 5) on the line 3x = 2y -15
L is a point on the line segment PQ dividing it in the ratio 1 : 3. If the coordinates of P and Q are (3, 7) and ( 11,-5) respectively, find if L lies on the line 2x + 5y = 20.
The line segment formed by two points A (2,3) and B (5, 6) is divided by a point in the ratio 1 : 2. Find, whether the point of intersection lies on the line 3x - 4y + 5 = 0.
Find the value of a line parallel to the following line:
`"x"/4 +"y"/3` = 1
Find the equation of a line whose slope and y-intercept are m = -3, c = -1
Find the equation of a line passing through the intersection of x + 2y + 1= 0 and 2x - 3y = 12 and perpendicular to the line 2x + 3y = 9
