Advertisements
Advertisements
प्रश्न
Find the equation of a line whose slope and y-intercept are m = -3, c = -1
उत्तर
m = -3, c = -1
y = mx + c
⇒ y = -3x -1
⇒ 3x + y + 1 = 0
APPEARS IN
संबंधित प्रश्न
A(2, 5), B(–1, 2) and C(5, 8) are the vertices of a triangle ABC, `M' is a point on AB such that AM: MB = 1: 2. Find the coordinates of 'M'. Hence find the equation of the line passing through the points C and M
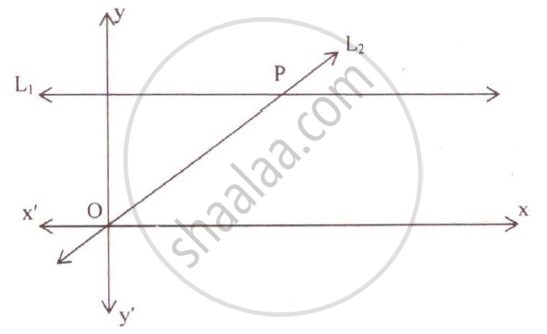
Given the equation of line L, is y = 4.
(1) Write the slope of line L2, if L2, is the bisector of angle O.
(2) Write the co–ordinates of point P.
(3) Find the equation of L2.
Find, which of the following points lie on the line x – 2y + 5 = 0 :
(2, –1.5)
The line given by the equation `2x - y/3 = 7` passes through the point (k, 6); calculate the value of k.
The line y = 3x – 2 bisects the join of (a, 3) and (2, −5), find the value of a.
A(1, 4), B(3, 2) and C(7, 5) are vertices of a triangle ABC. Find the co-ordinates of the centroid of triangle ABC.
Find the equation of a line passing through the point (2, 3) and having the x-intercept of 4 units.
Find the equation of a line passing through (2,9) and parallel to the line 3x + 4y = 11
Find the equation of a line which is inclined to x axis at an angle of 60° and its y – intercept = 2.
In the given diagram, OA = OB, ∠OAB = 𝜃 and the line AB passes through point P (-3, 4).
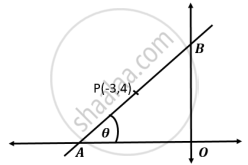
Find:
- Slope and inclination (𝜃) of the line AB
- Equation of the line AB
