Advertisements
Advertisements
प्रश्न
Find the equation of a line whose slope and y-intercept are m = -3, c = -1
उत्तर
m = -3, c = -1
y = mx + c
⇒ y = -3x -1
⇒ 3x + y + 1 = 0
APPEARS IN
संबंधित प्रश्न
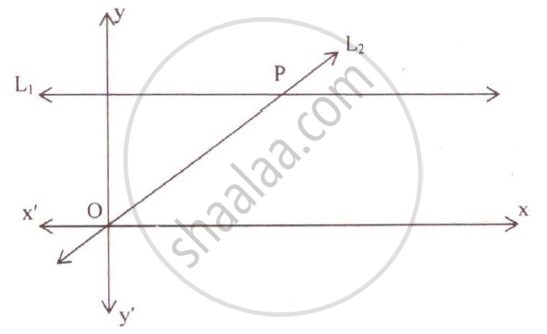
Given the equation of line L, is y = 4.
(1) Write the slope of line L2, if L2, is the bisector of angle O.
(2) Write the co–ordinates of point P.
(3) Find the equation of L2.
The line given by the equation `2x - y/3 = 7` passes through the point (k, 6); calculate the value of k.
Find the point of intersection of the lines 4x + 3y = 1 and 3x − y + 9 = 0. If this point lies on the line (2k – 1) x – 2y = 4; find the value of k.
In triangle ABC, the co-ordinates of vertices A, B and C are (4, 7), (–2, 3) and (0, 1) respectively. Find the equation of median through vertex A. Also, find the equation of the line through vertex B and parallel to AC.
Write down the equation of the line whose gradient is `-2/5` and which passes through point P, where P divides the line segement joining A(4, −8) and B(12, 0) in the ratio 3 : 1.
The vertices of a triangle ABC are A(0, 5), B(−1, −2) and C(11, 7). Write down the equation of BC. Find:
- the equation of line through A and perpendicular to BC.
- the co-ordinates of the point P, where the perpendicular through A, as obtained in (i), meets BC.
Find the equation of a line passing through the point (2, 3) and having the x-intercept of 4 units.
Find the equation of a line passing through (2,5) and making and angle of 30° with the positive direction of the x-axis.
The slope of aline joining P(6,k) and Q(1 - 3k, 3) is `1/2` Find
(i) k.
(ii) mid-point of PQ, using the value of 'k' found in (i).
PQ is straight line of 13 units. If P has coordinate (2, 5) and Q has coordinate (x, – 7) find the possible values of x.
