Advertisements
Advertisements
प्रश्न
In triangle ABC, the co-ordinates of vertices A, B and C are (4, 7), (–2, 3) and (0, 1) respectively. Find the equation of median through vertex A. Also, find the equation of the line through vertex B and parallel to AC.
उत्तर
Given, the co-ordinates of vertices A, B and C of a triangle ABC are (4, 7), (–2, 3) and (0, 1) respectively.
Let AD be the median through vertex A.
Co-ordinates of the point D are
`((-2 + 0)/2, (3 + 1)/2)`
(–1, 2)
∴ Slope of AD = `(2 - 7)/(-1 - 4) = (-5)/(-5) = 1`
The equation of the median AD is given by:
y − y1 = m(x − x1)
y − 2 = 1(x + 1)
y − 2 = x + 1
y = x + 3
The slope of the line which is parallel to line AC will be equal to the slope of AC.
Slope of AC = `(1 - 7)/(0 - 4) = (-6)/(-4) = 3/2`
The equation of the line which is parallel to AC and passes through B is given by:
`y - 3 = 3/2(x + 2)`
2y − 6 = 3x + 6
2y = 3x + 12
APPEARS IN
संबंधित प्रश्न
Show that the lines 2x + 5y = 1, x – 3y = 6 and x + 5y + 2 = 0 are concurrent.
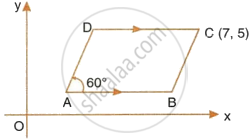
The following figure shows a parallelogram ABCD whose side AB is parallel to the x-axis, ∠A = 60° and vertex C = (7, 5). Find the equations of BC and CD.
Find the equations of the lines passing through point (–2, 0) and equally inclined to the co-ordinate axes.
A straight line passes through the point (3, 2) and the portion of this line, intercepted between the positive axes, is bisected at this point. Find the equation of the line.
Find the value of a line parallel to the following line:
x = `"y"/2` - 5
Find the value of a line parallel to the following line:
`(3"y")/4 + (5"y")/2 = 7`
ABCD is a square. The cooordinates of B and D are (-3, 7) and (5, -1) respectively. Find the equation of AC.
The coordinates of two points P and Q are (0,4) and (3,7) respectively. Find
(i) The gradient of PQ
(ii) the equation of PQ
(iii) the coordinates of the point where the line AB intersects the X-axis.
PQ is straight line of 13 units. If P has coordinate (2, 5) and Q has coordinate (x, – 7) find the possible values of x.
If the image of the point (2,1) with respect to the line mirror be (5, 2). Find the equation of the mirror.
