Advertisements
Advertisements
प्रश्न
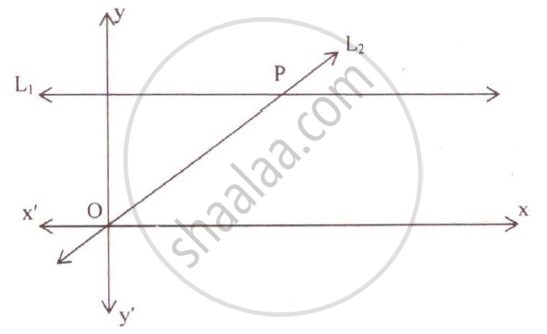
Given the equation of line L, is y = 4.
(1) Write the slope of line L2, if L2, is the bisector of angle O.
(2) Write the co–ordinates of point P.
(3) Find the equation of L2.
उत्तर
The equation of the line L1 is y = 4.
It is given that L2 is the bisector of angle O and ∠O = 90˚.
Thus, the line L2 makes an angle of 45˚ with the x-axis.
Thus, slope of line L2 = tan 45˚ = 1
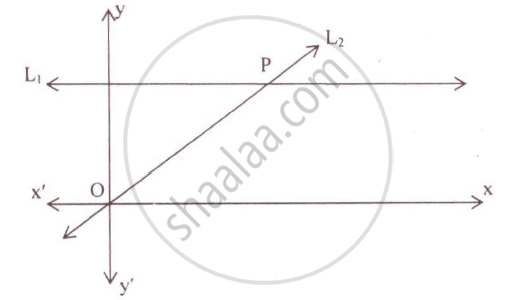
The line L2 passes through (0, 0) and its slope is 1. So, its equation is given by
y – y1 = m(x – x1)
y – 0 = 1(x – 0)
y = x
Now, the point P is the point of intersection of the lines L1 and L2.
Solving the equations y = 4 and x = y, we get x = y = 4
Thus, the coordinates of the point P are (4, 4).
APPEARS IN
संबंधित प्रश्न
Find the equation of the line passing through : (−1, −4) and (3, 0)
Find the equation of the line, whose x-intercept = −4 and y-intercept = 6
Find the equation of the line passing through the point of intersection of 7x + 6y = 71 and 5x – 8y = −23; and perpendicular to the line 4x – 2y = 1.
Find if the following points lie on the given line or not:
(1,3) on the line 2x + 3y = 11
Find the value of m if the line 2x + 5y + 12 = 0 passes through the point
( 4,m ).
The line segment formed by two points A (2,3) and B (5, 6) is divided by a point in the ratio 1 : 2. Find, whether the point of intersection lies on the line 3x - 4y + 5 = 0.
Find the inclination of a line whose gradient is 3.0777
Find the equation of a line passing through (-5,-1) and perpendicular to the 3x + y = 9
A(8,5), B (-2,1) and C(5,4) are the vertices of a triangle. Find the equation of the median of the traingle through C.
Find the equation of a straight line which cuts an intercept of 5 units on Y-axis and is parallel to the line joining the points (3, – 2) and (1, 4).
