Advertisements
Advertisements
प्रश्न
Find the value of m if the line 2x + 5y + 12 = 0 passes through the point
( 4,m ).
उत्तर
The line 2x + 5y + 12 = 0 passes through (4,m)
(4,m) will satisfy the equation of line
2(4) + 5(m) + 12 = 0
8 + 5m + 12 = 0
5m + 20 = 0
m = `(-20)/5`
`therefore` m = -4
APPEARS IN
संबंधित प्रश्न
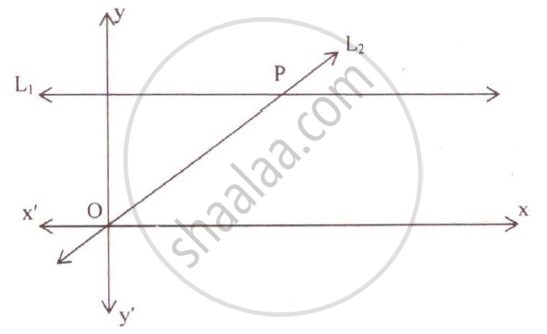
Given the equation of line L, is y = 4.
(1) Write the slope of line L2, if L2, is the bisector of angle O.
(2) Write the co–ordinates of point P.
(3) Find the equation of L2.
Find, which of the following points lie on the line x – 2y + 5 = 0 :
(1, 3)
Find the point of intersection of the lines 4x + 3y = 1 and 3x − y + 9 = 0. If this point lies on the line (2k – 1) x – 2y = 4; find the value of k.
The co-ordinates of two points P and Q are (2, 6) and (−3, 5) respectively Find the co-ordinates of the point where PQ intersects the x-axis.
Find the equation of the line, whose x-intercept = −8 and y-intercept = −4
A(1, 4), B(3, 2) and C(7, 5) are vertices of a triangle ABC. Find the equation of a line, through the centroid and parallel to AB.
The line 5x + 3y = 25 divides the join of (b,4) and (5, 8) in the ratio of 1 : 3. Find the value of b.
Find the equation of a line whose slope and y-intercept are m = `(-1)/2`, c = 5
Find the equation of a line passing through (2,9) and parallel to the line 3x + 4y = 11
Find the equation of the line passing through (0, 4) and parallel to the line 3x + 5y + 15 = 0.
