Advertisements
Advertisements
प्रश्न
Find the value of p if the line 3y = 5x - 7 passes through the point (p,6).
उत्तर
The line 3y = 5x - 7 passes through (p,6)
(p,6) will satisfy the equation of line
3( 6) = 5(p) - 7
⇒ 25 =5p
⇒ p= 5
APPEARS IN
संबंधित प्रश्न
Find the equations of the lines passing through point (–2, 0) and equally inclined to the co-ordinate axes.
A(1, 4), B(3, 2) and C(7, 5) are vertices of a triangle ABC. Find the co-ordinates of the centroid of triangle ABC.
The vertices of a triangle ABC are A(0, 5), B(−1, −2) and C(11, 7). Write down the equation of BC. Find:
- the equation of line through A and perpendicular to BC.
- the co-ordinates of the point P, where the perpendicular through A, as obtained in (i), meets BC.
Write down the equation of the line whose gradient is `3/2` and which passes through P, where P divides the line segment joining A(−2, 6) and B(3, −4) in the ratio 2 : 3.
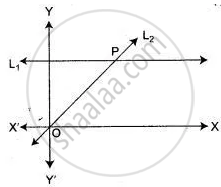
Given equation of line L1 is y = 4.
- Write the slope of line L2 if L2 is the bisector of angle O.
- Write the co-ordinates of point P.
- Find the equation of L2.
Find if the following points lie on the given line or not:
(5,3) on the line 3x - 5y + 5 = 0
The line segment formed by two points A (2,3) and B (5, 6) is divided by a point in the ratio 1 : 2. Find, whether the point of intersection lies on the line 3x - 4y + 5 = 0.
PQ is straight line of 13 units. If P has coordinate (2, 5) and Q has coordinate (x, – 7) find the possible values of x.
Find the equation of the straight line which has Y-intercept equal to 4/3 and is perpendicular to 3x – 4y + 11 = 0.
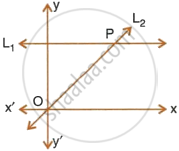
Given equation of line L1 is y = 4.
(i) Write the slope of line, if L2 is the bisector of angle O.
(ii) Write the coordinates of point P.
(iii) Find the equation of L2