Advertisements
Advertisements
प्रश्न
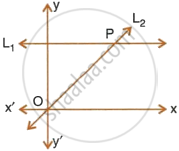
Given equation of line L1 is y = 4.
- Write the slope of line L2 if L2 is the bisector of angle O.
- Write the co-ordinates of point P.
- Find the equation of L2.
उत्तर
i. Equation of line L1 is y = 4
∵ L2 is the bisector of ∠O
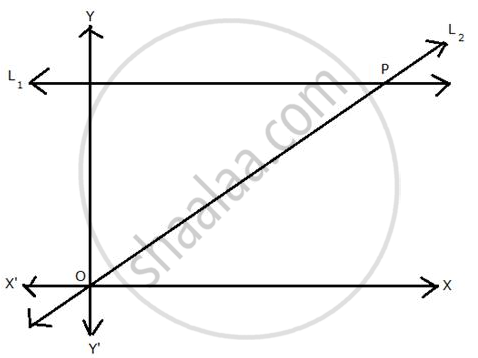
∴ ∠POX = 45°
Slope = tan 45° = 1 ...(i)
Let coordinates of P be (x, y)
∵ P lies on L1
ii. ∴ Slope of L2 = `(y_2 - y_1)/(x_2 -x_1)`
`1 = (4 - 0)/(x - 0)`
`=> 1 = 4/x` ...(ii)
From equation (i) and (ii)
`1 = 4/x`
`=>` x = 4
∴ Coordinates of P are (4, 4)
iii. Equation of L2 is
y – y1 = m(x – x1)
`=>` y – 4 = 1(x – 4)
`=>` y – 4 = x – 4
`=>` x = y
APPEARS IN
संबंधित प्रश्न
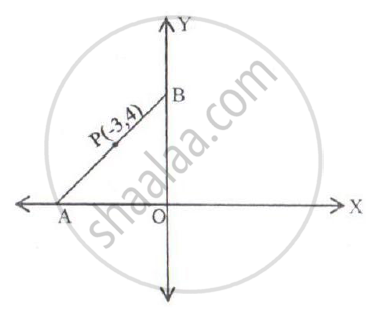
In the figure given below, the line segment AB meets X-axis at A and Y-axis at B. The point P(-3, 4) on AB divides it in the ratio 2:3. Find the coordinates of A and B.
The equation of a line 3x + 4y − 7 = 0. Find
1) The slope of the line.
2) The equation of a line perpendicular to the given line and passing through the intersection of the lines x – y + 2 = 0 and 3x + y – 10 = 0.
State, true or false :
If the point (2, a) lies on the line 2x – y = 3, then a = 5.
The line segment joining the points A(3, −4) and B(−2, 1) is divided in the ratio 1 : 3 at point P in it. Find the co-ordinates of P. Also, find the equation of the line through P and perpendicular to the line 5x – 3y = 4.
Determine whether the line through points (–2, 3) and (4, 1) is perpendicular to the line 3x = y + 1.
Does line 3x = y + 1 bisect the line segment joining the two given points?
The line 5x - 3y +1 = 0 divides the join of (2,m) and (7,9) in the ratio 2: 3. Find the value of m.
Find the equations of a line passing through the point (2, 3) and having the x – interecpt of 4 units.
Find the equation of the straight line perpendicular to 5x – 2y = 8 and which passes through the mid-point of the line segment joining (2, 3) and (4, 5).
Find the equation of a straight line which cuts an intercept – 2 units from Y-axis and being equally inclined to the axis.
In the given diagram, OA = OB, ∠OAB = 𝜃 and the line AB passes through point P (-3, 4).
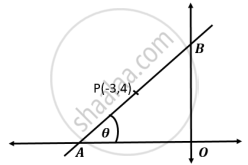
Find:
- Slope and inclination (𝜃) of the line AB
- Equation of the line AB
