Advertisements
Advertisements
Question
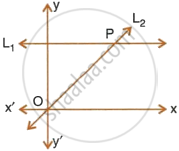
Given equation of line L1 is y = 4.
- Write the slope of line L2 if L2 is the bisector of angle O.
- Write the co-ordinates of point P.
- Find the equation of L2.
Solution
i. Equation of line L1 is y = 4
∵ L2 is the bisector of ∠O
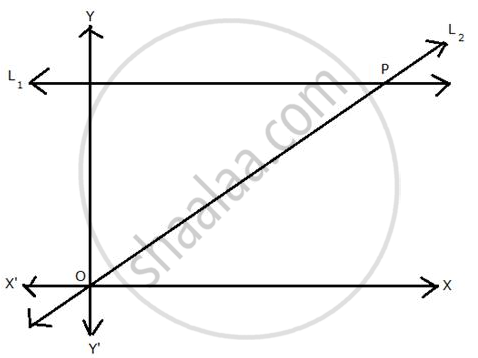
∴ ∠POX = 45°
Slope = tan 45° = 1 ...(i)
Let coordinates of P be (x, y)
∵ P lies on L1
ii. ∴ Slope of L2 = `(y_2 - y_1)/(x_2 -x_1)`
`1 = (4 - 0)/(x - 0)`
`=> 1 = 4/x` ...(ii)
From equation (i) and (ii)
`1 = 4/x`
`=>` x = 4
∴ Coordinates of P are (4, 4)
iii. Equation of L2 is
y – y1 = m(x – x1)
`=>` y – 4 = 1(x – 4)
`=>` y – 4 = x – 4
`=>` x = y
APPEARS IN
RELATED QUESTIONS
The co-ordinates of two points P and Q are (2, 6) and (−3, 5) respectively. Find:
- the gradient of PQ;
- the equation of PQ;
- the co-ordinates of the point where PQ intersects the x-axis.
Find the equation of the perpendicular dropped from the point (−1, 2) onto the line joining the points (1, 4) and (2, 3).
A line 5x + 3y + 15 = 0 meets y-axis at point P. Find the co-ordinates of points P. Find the equation of a line through P and perpendicular to x – 3y + 4 = 0.
A straight line passes through the point (3, 2) and the portion of this line, intercepted between the positive axes, is bisected at this point. Find the equation of the line.
Find the value of m if the line 2x + 5y + 12 = 0 passes through the point
( 4,m ).
The line 2x - 5y + 31 = 0 bisects the join of (-4,5) and (P, 9). Find the value of p.
The line 5x + 3y = 25 divides the join of (b,4) and (5, 8) in the ratio of 1 : 3. Find the value of b.
Find the inclination of a line whose gradient is 5.6713
If the image of the point (2,1) with respect to the line mirror be (5, 2). Find the equation of the mirror.
ABC is a triangle whose vertices are A(1, –1), B(0, 4) and C(– 6, 4). D is the midpoint of BC. Find the equation of the median AD.
