Advertisements
Advertisements
Question
The line 5x + 3y = 25 divides the join of (b,4) and (5, 8) in the ratio of 1 : 3. Find the value of b.
Solution
Let the point of intersection of PQ and the line 5x+3y=25, be the point R(x,y)
Also, given the line 5x + 3y = 25 divides the line segment PQ in the ratio 1 :3.
i.e. PR : RQ = 1 : 3
Coordinates of Rare,
R (x,y) = R `((5 + 3"b")/4 , (8 + 12)/4) = "R" ((5 + 3"b" )/4 , 5)`
R (x,y) lies on the line 5x + 3y = 25
R will satisfy the equation of the line
5`((5 + 3"b")/4)` + 3 (5) = 25
⇒ 5`((5 + 3"b")/4)` = 10
⇒ 5 + 3b = 8
⇒ 3b = 3
⇒ b = 1
APPEARS IN
RELATED QUESTIONS
The co-ordinates of two points P and Q are (2, 6) and (−3, 5) respectively. Find:
- the gradient of PQ;
- the equation of PQ;
- the co-ordinates of the point where PQ intersects the x-axis.
The co-ordinates of two points P and Q are (2, 6) and (−3, 5) respectively Find the co-ordinates of the point where PQ intersects the x-axis.
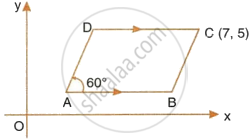
The following figure shows a parallelogram ABCD whose side AB is parallel to the x-axis, ∠A = 60° and vertex C = (7, 5). Find the equations of BC and CD.
Find the value of p if the line 3y = 5x - 7 passes through the point (p,6).
Find the inclination of a line whose gradient is 0.4663
Find the equation of a line passing through the intersection of x + 3y = 6 and 2x - 3y = 12 and parallel to the line 5x + 2y = 10
Find a general equation of a line which passes through:
(i) (0, -5) and (3, 0) (ii) (2, 3) and (-1, 2).
Find the equation of the line passing through (0, 4) and parallel to the line 3x + 5y + 15 = 0.
Find the equation of a line passing through (3, – 2) and perpendicular to the line.
x - 3y + 5 = 0.
ABC is a triangle whose vertices are A(1, –1), B(0, 4) and C(– 6, 4). D is the midpoint of BC. Find the equation of the median AD.
