Advertisements
Advertisements
Question
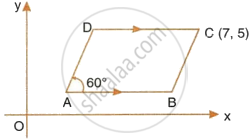
The following figure shows a parallelogram ABCD whose side AB is parallel to the x-axis, ∠A = 60° and vertex C = (7, 5). Find the equations of BC and CD.
Solution
Since, ABCD is a parallelogram,
∠A + ∠B = 180°
∠B = 180° – 60° = 120°
Slope of BC = tan 120° = tan (90° + 30°) = cot 30° = `sqrt(3)`
Equation of the line BC is given by:
y − y1 = m(x − x1)
`y - 5 = sqrt(3)(x - 7)`
`y - 5 = sqrt(3)x - 7sqrt(3)`
`y = sqrt(3)x + 5 - 7sqrt(3)`
Since, CD || AB and AB || x-axis, slope of CD = Slope of AB = 0
Equation of the line CD is given by:
y − y1 = m(x − x1)
y − 5 = 0(x − 7)
y = 5
APPEARS IN
RELATED QUESTIONS
Find, which of the following points lie on the line x – 2y + 5 = 0 :
(0, 5)
State, true or false :
The point (–3, 0) lies on the line x + 3 = 0
The line segment joining the points (5, −4) and (2, 2) is divided by the points Q in the ratio 1 : 2. Does the line x – 2y = 0 contain Q?
Find the equation of the line, whose x-intercept = 5 and y-intercept = 3
Find the equation of the line, whose x-intercept = −4 and y-intercept = 6
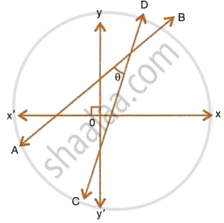
The given figure (not drawn to scale) shows two straight lines AB and CD. If equation of the line AB is : y = x + 1 and equation of line CD is : y = `sqrt(3)x - 1`. Write down the inclination of lines AB and CD; also, find the angle θ between AB and CD.
The vertices of a ΔABC are A(3, 8), B(–1, 2) and C(6, –6). Find:
(i) Slope of BC
(ii) Equation of a line perpendicular to BC and passing through A.
Find the equation of a line passing through the intersection of x + 3y = 6 and 2x - 3y = 12 and parallel to the line 5x + 2y = 10
Find the value of ‘a’ for which the following points A (a, 3), B (2, 1) and C (5, a) are collinear. Hence find the equation of the line.
Which of the following equation represents a line equally inclined to the axes?
