Advertisements
Advertisements
Question
The given figure (not drawn to scale) shows two straight lines AB and CD. If equation of the line AB is : y = x + 1 and equation of line CD is : y = `sqrt(3)x - 1`. Write down the inclination of lines AB and CD; also, find the angle θ between AB and CD.
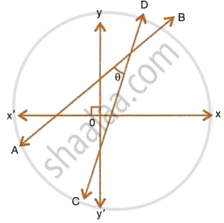
Solution
Equation of the line AB is y = x + 1
Slope of AB = 1
Inclination of line AB = 45° ...(Since, tan 45° = 1)
`=>` ∠RPQ = 45°
Equation of line CD is y = `sqrt(3)x - 1`
Slope of CD = `sqrt(3)`
Inclination of line CD = 60° ...(Since, tan 60° = `sqrt(3)`)
`=>` ∠DQX = 60°
∴ ∠DQP = 180° – 60° = 120°
Using angle sum property in ∆PQR,
θ = 180° – 45° – 120° = 15°
APPEARS IN
RELATED QUESTIONS
Find, which of the following points lie on the line x – 2y + 5 = 0 :
(2, –1.5)
The co-ordinates of two points A and B are (–3, 4) and (2, –1). Find:
- the equation of AB;
- the co-ordinates of the point where the line AB intersects the y-axis.
Write down the equation of the line whose gradient is `-2/5` and which passes through point P, where P divides the line segement joining A(4, −8) and B(12, 0) in the ratio 3 : 1.
The vertices of a ΔABC are A(3, 8), B(–1, 2) and C(6, –6). Find:
(i) Slope of BC
(ii) Equation of a line perpendicular to BC and passing through A.
Find the equation of a line passing through (2,5) and making and angle of 30° with the positive direction of the x-axis.
Find the equation of a line passing through (-5,-1) and perpendicular to the 3x + y = 9
ABCD is a square. The cooordinates of B and D are (-3, 7) and (5, -1) respectively. Find the equation of AC.
P(5,3), Q(-4,7) and R(8,3) are he vertices of a traingles. Find the equation of the median of the traiangle from p.
Find a general equation of a line which passes through:
(i) (0, -5) and (3, 0) (ii) (2, 3) and (-1, 2).
ABC is a triangle whose vertices are A(1, –1), B(0, 4) and C(– 6, 4). D is the midpoint of BC. Find the equation of the median AD.
