Advertisements
Advertisements
प्रश्न
Find the value of a for which the points A(a, 3), B(2, 1) and C(5, a) are collinear. Hence, find the equation of the line.
उत्तर
If 3 points are collinear, the slope between any 2 points is the same.
Thus, for A(a, 3), B(2, 1) and C(5, a) to be collinear, the slope Between A and B and between B and C should be the same.
`=> (1 - 3)/(2 - a) = (a - 1)/(5 - 2)`
`=> (-2)/(2 - a) = (a - 1)/3`
`=> 2/(a - 2) = (a - 1)/3`
`=>` 6 = (a – 2)(a – 1)
`=>` a2 – 3a + 2 = 6
`=>` a2 – 3a – 4 = 0
`=>` a = –1 or 4
Thus, slope can be:
`2/(a - 2) = 2/(-1 -2) = -2/3` OR `2/(a - 2) = 2/(4 - 2) = 1`
Thus, the equation of the line can be:
`(y - 1)/(x -2) = - 2/3`
Equation of line
`=>` y – y1 = m(x – x1)
`=> y - 3 = (-2)/3[x - (-1)]`
`=>` 3(y – 3) = –2(x + 1)
`=>` 3y – 9 = –2x – 2
`=>` 2x + 3y = –2 + 9
`=>` 2x + 3y = 7
or
`(y - 1)/(x - 2) = 1`
`=>` y – x = –1
`=>` x – y = 1
APPEARS IN
संबंधित प्रश्न
The point (−3, 2) lies on the line ax + 3y + 6 = 0, calculate the value of a.
The co-ordinates of two points P and Q are (2, 6) and (−3, 5) respectively Find the co-ordinates of the point where PQ intersects the x-axis.
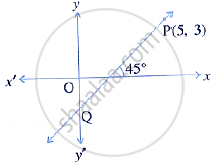
The line through P (5, 3) intersects y-axis at Q.
Find the co-ordinates of Q.
Find the value of p if the line 3y = 5x - 7 passes through the point (p,6).
P is a point on the line segment AB dividing it in the ratio 2 : 3. If the coordinates of A and Bare (-2,3) and (8,8), find if Plies on the line 7x - 2y =4.
Find the inclination of a line whose gradient is 0.4663
Find the inclination of a line whose gradient is 1.4281
A(8,5), B (-2,1) and C(5,4) are the vertices of a triangle. Find the equation of the median of the traingle through C.
Find the equation of the line passing through (0, 4) and parallel to the line 3x + 5y + 15 = 0.
Find the equation of the straight line perpendicular to 5x – 2y = 8 and which passes through the mid-point of the line segment joining (2, 3) and (4, 5).
