Advertisements
Advertisements
Question
L is a point on the line segment PQ dividing it in the ratio 1 : 3. If the coordinates of P and Q are (3, 7) and ( 11,-5) respectively, find if L lies on the line 2x + 5y = 20.
Solution
Let L(a,b) be the point on line segment PQ dividing it in the ratio 1 : 3
i.e. PL : LQ = 1 : 3
Coordinates of L are,
L (a,b) = L `((11 + 9)/4 , (-5 + 21)/4)`
= L (5,4)
If L(a,b) lies on the line 2x + 5y = 20, then it wll satisfy the equation of the line
LHS = 2 (5) + 5 (4) = 10 + 20 = 30 ≠ RHS
No, L (a,b) does not lie on the line 2x + 5y = 20
APPEARS IN
RELATED QUESTIONS
A(-1, 3), B(4, 2) and C(3, -2) are the vertices of a triangle.
1) Find the coordinates of the centroid G of the triangle
2) Find the equation of the line through G and parallel to AC
Solve the following inequation and represent the solution set on the number line 2x – 5 <= 5x + 4 < 11, where x ∈ I
Find, which of the following points lie on the line x – 2y + 5 = 0 :
(–5, 0)
Find the equation of a line whose : y-intercept = −1 and inclination = 45°
Find the equation of the line whose slope is `-4/3` and which passes through (−3, 4).
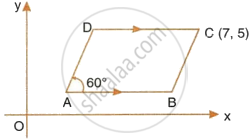
The following figure shows a parallelogram ABCD whose side AB is parallel to the x-axis, ∠A = 60° and vertex C = (7, 5). Find the equations of BC and CD.
In triangle ABC, the co-ordinates of vertices A, B and C are (4, 7), (–2, 3) and (0, 1) respectively. Find the equation of median through vertex A. Also, find the equation of the line through vertex B and parallel to AC.
A line intersects x-axis at point (−2, 0) and cuts off an intercept of 3 units from the positive side of y-axis. Find the equation of the line.
Find the equation of a line whose slope and y-intercept are m = -3, c = -1
ABCD is a square. The cooordinates of B and D are (-3, 7) and (5, -1) respectively. Find the equation of AC.
