Advertisements
Advertisements
प्रश्न
L is a point on the line segment PQ dividing it in the ratio 1 : 3. If the coordinates of P and Q are (3, 7) and ( 11,-5) respectively, find if L lies on the line 2x + 5y = 20.
उत्तर
Let L(a,b) be the point on line segment PQ dividing it in the ratio 1 : 3
i.e. PL : LQ = 1 : 3
Coordinates of L are,
L (a,b) = L `((11 + 9)/4 , (-5 + 21)/4)`
= L (5,4)
If L(a,b) lies on the line 2x + 5y = 20, then it wll satisfy the equation of the line
LHS = 2 (5) + 5 (4) = 10 + 20 = 30 ≠ RHS
No, L (a,b) does not lie on the line 2x + 5y = 20
APPEARS IN
संबंधित प्रश्न
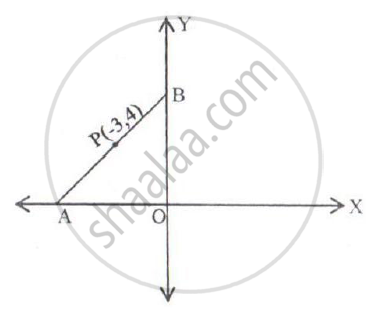
In the figure given below, the line segment AB meets X-axis at A and Y-axis at B. The point P(-3, 4) on AB divides it in the ratio 2:3. Find the coordinates of A and B.
The point (−3, 2) lies on the line ax + 3y + 6 = 0, calculate the value of a.
Find the point of intersection of the lines 4x + 3y = 1 and 3x − y + 9 = 0. If this point lies on the line (2k – 1) x – 2y = 4; find the value of k.
Find the equation of the line whose slope is `-4/3` and which passes through (−3, 4).
The co-ordinates of two points A and B are (–3, 4) and (2, –1). Find:
- the equation of AB;
- the co-ordinates of the point where the line AB intersects the y-axis.
The line segment joining the points A(3, −4) and B(−2, 1) is divided in the ratio 1 : 3 at point P in it. Find the co-ordinates of P. Also, find the equation of the line through P and perpendicular to the line 5x – 3y = 4.
A line intersects x-axis at point (−2, 0) and cuts off an intercept of 3 units from the positive side of y-axis. Find the equation of the line.
Find if the following points lie on the given line or not:
(2,4) on the line y = 2x - 1
Find the equation of a line which is inclined to x axis at an angle of 60° and its y – intercept = 2.
A and B are two points on the x-axis and y-axis respectively.

- Write down the coordinates of A and B.
- P is a point on AB such that AP : PB = 1 : 1.
Using section formula find the coordinates of point P. - Find the equation of a line passing through P and perpendicular to AB.
