Advertisements
Advertisements
Question
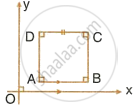
The side AB of a square ABCD is parallel to the x-axis. Find the slopes of all its sides. Also, find:
- the slope of the diagonal AC.
- the slope of the diagonal BD.
Solution
We know that the slope of any line parallel to x-axis is 0.
Therefore, slope of AB = 0
As CD || BC, slope of CD = Slope of AB = 0
As BC ⊥ AB, slope of BC = `-1/"slope of AB"` = `(-1)/0` = not defined
As AD ⊥ AB, slope of AD = `-1/"slope of AB"` = `(-1)/0` = not defined
i. The diagonal AC makes an angle of 45° with the positive direction of x-axis.
∴ Slope of AC = tan 45° = 1
ii. The diagonal BD makes an angle of – 45° with the positive direction of x-axis.
∴ Slope of BD = tan (– 45°) = −1
APPEARS IN
RELATED QUESTIONS
Find the slope and the inclination of the line AB if : A = (−3, −2) and B = (1, 2)
The points (−3, 2), (2, −1) and (a, 4) are collinear. Find a.
Find the value(s) of k so that PQ will be parallel to RS. Given : P(3, −1), Q(7, 11), R(−1, −1) and S(1, k)
The lines represented by 4x + 3y = 9 and px – 6y + 3 = 0 are parallel. Find the value of p.
Determine whether the following point is collinear.
R(1, –4), S(–2, 2), T(–3, 4)
Find the slope of a line parallel to the given line x +3y = 7
Find the slope of the line passing through the points M(4,0) and N(-2,-3).
Given that (a, 2a) lies on line`(y)/(2) = 3 - 6`.Find the value of a.
Determine whether the following points are collinear. A(–1, –1), B(0, 1), C(1, 3)
Given: Points A(–1, –1), B(0, 1) and C(1, 3)
Slope of line AB = `(square - square)/(square - square) = square/square` = 2
Slope of line BC = `(square - square)/(square - square) = square/square` = 2
Slope of line AB = Slope of line BC and B is the common point.
∴ Points A, B and C are collinear.
