Advertisements
Advertisements
Question
Is the line 3x + 4y + 7 = 0 perpendicular to the line 28x – 21y + 50 = 0?
Solution
3x + 4y + 7 = 0
`=>` 4y = –3x – 7
`=> y = -3/4 xx -7/4`
Slope of this line = `(-3)/4`
28x – 21y + 50 = 0
`=>` 21y = 28x + 50
`=> y = 28/21x + 50/21`
`=> y = 4/3x + 50/21`
Slope of this line = `4/3`
Since, product of slopes of the two lines = –1, the lines are perpendicular to each other.
APPEARS IN
RELATED QUESTIONS
A (5, 4), B (-3, -2) and C (1, -8) are the vertices of a triangle ABC. Find the equations of the median AD and line parallel to AC passing through the point B.
Find the slope and y-intercept of the line:
3x – 4y = 5
Find the equation of the perpendicular bisector of the line segment obtained on joining the points (6, −3) and (0, 3).
The line 4x − 3y + 12 = 0 meets x-axis at A. Write the co-ordinates of A. Determine the equation of the line through A and perpendicular to 4x – 3y + 12 = 0.
The point P is the foot of perpendicular from A(−5, 7) to the line whose equation is 2x – 3y + 18 = 0. Determine :
- the equation of the line AP.
- the co-ordinates of P.
Show that points P(2, –2), Q(7, 3), R(11, –1) and S (6, –6) are vertices of a parallelogram.
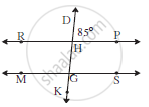
In the adjoining figure line RP ||line MS , line DK is a transversal . If ∠DHP = 85° find ∠RHG and ∠HGS.
Find Equation of CD
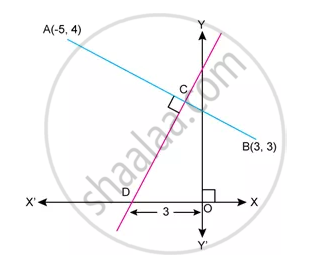
Find the equation of the line that has x-intercept = –3 and is perpendicular to 3x + 5y = 1.
Find the equation of the line passing through the points (4,-5) and (-1,-2).
