Advertisements
Advertisements
Question
Find Equation of CD
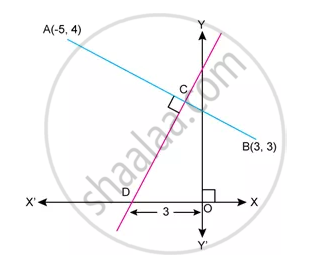
Solution
AB and CD are Perpendicular to each other.
Thus,Product of their slops=-1
`"Slope of AB" xx "Slop of CD"=-1`
⇒ Slope of CD=8
Now, from graph we have coordinates of `D=(-3,0)`
∴ Equation of line CD is given by
`y-0=8(x-3)`
`y=8x +24`
APPEARS IN
RELATED QUESTIONS
The equation of a line is x – y = 4. Find its slope and y-intercept. Also, find its inclination.
Is the line x – 3y = 4 perpendicular to the line 3x – y = 7?
- Write down the equation of the line AB, through (3, 2) and perpendicular to the line 2y = 3x + 5.
- AB meets the x-axis at A and the y-axis at B. Write down the co-ordinates of A and B. Calculate the area of triangle OAB, where O is the origin.
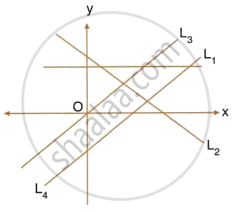
Match the equations A, B, C and D with the lines L1, L2, L3 and L4, whose graphs are roughly drawn in the given diagram.
A ≡ y = 2x;
B ≡ y – 2x + 2 = 0;
C ≡ 3x + 2y = 6;
D ≡ y = 2
Find the point on the X–axis which is equidistant from A(–3, 4) and B(1, –4).
Verify that points P(–2, 2), Q(2, 2) and R(2, 7) are vertices of a right angled triangle.
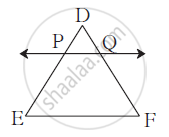
In Δ DEF, line PQ || side EF, If DP = 2.4,
PE = 7.2, DQ = 1 then find QF.
Prove that :
“If a line parallel to a side of a triangle intersects the remaining sides in two distince points, then the line divides the sides in the same proportion.”
Find the equation of the line through the points A(–1, 3) and B(0, 2). Hence, show that the point A, B and C(1, 1) are collinear.
A line segment joining P(2, –3) and Q(0, –1) is cut by the x-axis at the point R. A line AB cuts the y-axis at T(0, 6) and is perpendicular to PQ at S.
Find the:
- equation of line PQ
- equation of line AB
- coordinates of points R and S.
