Advertisements
Advertisements
Question
The point P is the foot of perpendicular from A(−5, 7) to the line whose equation is 2x – 3y + 18 = 0. Determine :
- the equation of the line AP.
- the co-ordinates of P.
Solution
i. The given equation is
2x − 3y + 18 = 0
3y = 2x + 18
`y = 2/3 x + 6`
Slope of this line = `2/3`
Slope of a line perpendicular to this line
= `(-1)/(2/3)`
= `(-3)/2`
(x1, y1) = (−5, 7)
The required equation of the line AP is given by
y − y1 = m(x − x1)
`y - 7 = (-3)/2 (x + 5)`
2y − 14 = −3x − 15
3x + 2y + 1 = 0
ii. P is the foot of perpendicular from point A.
So P is the point of intersection of the lines 2x − 3y + 18 = 0 and 3x + 2y + 1 = 0.
2x − 3y + 18 = 0
`=>` 4x − 6y + 36 = 0
3x + 2y + 1 = 0
`=>` 9x + 6y + 3 = 0
Adding the two equations, we get,
13x + 39 = 0
x = −3
∴ 3y = 2x + 18
= −6 + 18
= 12
y = 4
Thus, the co-ordinates of the point P are (−3, 4).
APPEARS IN
RELATED QUESTIONS
If (4,-3) is a point on the line AB and slope of the line is (-2), write the equation of the line AB.
In ΔABC, A(3, 5), B(7, 8) and C(1, –10). Find the equation of the median through A.
Given 3x + 2y + 4 = 0
(i) express the equation in the form y = mx + c
(ii) Find the slope and y-intercept of the line 3x + 2y + 4 = 0
Is the line 3x + 4y + 7 = 0 perpendicular to the line 28x – 21y + 50 = 0?
Find the equation of the line passing through (−2, 1) and perpendicular to 4x + 5y = 6.
A (5, 4), B (–3,–2) and C (1,–8) are the vertices of a triangle ABC. Find the equation of median AD and line parallel to AB passing through point C.
Find the point on the X–axis which is equidistant from A(–3, 4) and B(1, –4).
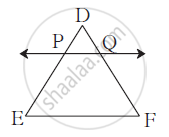
In Δ DEF, line PQ || side EF, If DP = 2.4,
PE = 7.2, DQ = 1 then find QF.
Line PQ is parallel to line RS where points P,Q,R and S have
co-ordinates (2, 4), (3, 6), (3, 1) and (5, k) respectively. Find value of k.
Find the equation of line through the intersection of lines 2x – y = 1 and 3x + 2y = –9 and making an angle of 30° with positive direction of x-axis.
