Advertisements
Advertisements
Question
Given a straight line x cos 30° + y sin 30° = 2. Determine the equation of the other line which is parallel to it and passes through (4, 3).
Solution
x cos 30° + y sin 30° = 2
`=> x sqrt(3)/2 + y + 1/2 = 2`
`=> sqrt(3)x + y = 4`
`=> y = -sqrt(3)x + 4`
Slope of this line = `-sqrt(3)`
Slope of a line which is parallel to this given line = `-sqrt(3)`
Let (4, 3) = (x1, y1)
Thus, the equation of the required line is given by :
y – y1 = m(x – x1)
`=> y - 3 = -sqrt(3) (x - 4) = -sqrt(3)x + 4sqrt(3)`
`=> sqrt(3)x + y = 4sqrt(3) + 3`
APPEARS IN
RELATED QUESTIONS
Find the equation of the line parallel to the line 3x + 2y = 8 and passing through the point (0, 1).
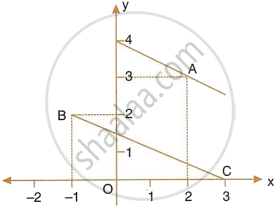
In the following diagram, write down:
- the co-ordinates of the points A, B and C.
- the equation of the line through A and parallel to BC.
A(1, −5), B(2, 2) and C(−2, 4) are the vertices of triangle ABC. Find the equation of the altitude of the triangle through B.
From the given figure, find:
- the co-ordinates of A, B and C.
- the equation of the line through A and parallel to BC.

Find the slope of a line perpendicular to the foloowing line `"x"/2 + "y"/3 = 4/3`
Find the value of a line perpendicular to the given line 2x-3y = 4
Find the value of a line perpendicular to the given line x-4y = 8
Find the value of a line perpendicular to the given line 9x-3y = 5
The lines px + 5y + 7 = 0 and 2y = 5x - 6 are perpendicular to ach other. Find p.
The lines 3x - 2y + 4 = 0 and 3x + my + 6 = 0 are parallel to each other . Find m.
