Advertisements
Advertisements
Question
Find the slope of the line perpendicular to AB if : A = (3, −2) and B = (−1, 2)
Solution
Slope of AB = `(2 + 2)/(-1 - 3)`
Slope of AB = `4/(-4)`
Slope of AB = –1
Slope of the line perpendicular to AB = `(-1)/"Slope of AB"`
Slope of the line perpendicular to AB = `(-1)/(-1)`
Slope of the line perpendicular to AB = 1
APPEARS IN
RELATED QUESTIONS
Find the slope of the line passing through the points A(-2, 1) and B(0, 3).
Find the value(s) of k so that PQ will be parallel to RS. Given : P(3, −1), Q(7, 11), R(−1, −1) and S(1, k)
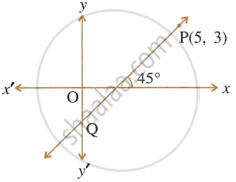
The line through P(5, 3) intersects y-axis at Q.
- Write the slope of the line.
- Write the equation of the line.
- Find the co-ordinates of Q.
Determine x so that the slope of the line through (1, 4) and (x, 2) is 2.
The line through A(−2, 3) and B(4, b) is perpendicular to the line 2x – 4y = 5. Find the value of b.
Find k, if B(k, –5), C (1, 2) and slope of the line is 7.
With out Pythagoras theorem, show that A(4, 4), B(3, 5) and C(-1, -1) are the vertices of a right angled.
The vertices of a triangle are A(10, 4), B(- 4, 9) and C(- 2, -1). Find the
If A(6, 1), B(8, 2), C(9, 4) and D(7, 3) are the vertices of `square`ABCD, show that `square`ABCD is a parallelogram.
Solution:
Slope of line = `("y"_2 - "y"_1)/("x"_2 - "x"_1)`
∴ Slope of line AB = `(2 - 1)/(8 - 6) = square` .......(i)
∴ Slope of line BC = `(4 - 2)/(9 - 8) = square` .....(ii)
∴ Slope of line CD = `(3 - 4)/(7 - 9) = square` .....(iii)
∴ Slope of line DA = `(3 - 1)/(7 - 6) = square` .....(iv)
∴ Slope of line AB = `square` ......[From (i) and (iii)]
∴ line AB || line CD
∴ Slope of line BC = `square` ......[From (ii) and (iv)]
∴ line BC || line DA
Both the pairs of opposite sides of the quadrilateral are parallel.
∴ `square`ABCD is a parallelogram.
Show that points A(– 4, –7), B(–1, 2), C(8, 5) and D(5, – 4) are the vertices of a parallelogram ABCD
