Advertisements
Advertisements
Question
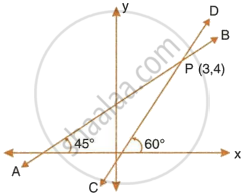
The figure given alongside shows two straight lines AB and CD intersecting each other at point P(3, 4). Find the equations of AB and CD.
Solution
Slope of line AB = tan 45° = 1
The line AB passes through P(3, 4).
So, the equation of the line AB is given by:
y − y1 = m(x − x1)
y − 4 = 1(x − 3)
y − 4 = x − 3
y = x + 1
Slope of line CD = tan 60° = `sqrt(3)`
The line CD passes through P(3, 4).
So, the equation of the line CD is given by:
y − y1 = m(x − x1)
`y - 4 = sqrt(3)(x − 3)`
`y - 4 = sqrt(3)x − 3sqrt(3)`
`y = sqrt(3)x + 4 − 3sqrt(3)`
APPEARS IN
RELATED QUESTIONS
If the straight lines 3x – 5y = 7 and 4x + ay + 9 = 0 are perpendicular to one another, find the value of a.
Find the equation of a line which passes through (5, 4) and makes an angle of 60° with the positive direction of the x-axis.
Find the equation of the line passing through : (−1, −4) and (3, 0)
A, B and C have co-ordinates (0, 3), (4, 4) and (8, 0) respectively. Find the equation of the line through A and perpendicular to BC.
Find the equation of the line with x-intercept 5 and a point on it (–3, 2).
The line through P (5, 3) intersects y-axis at Q.
write the equation of the line
A(7, −1), B(4, 1) and C(−3, 4) are the vertices of a triangle ABC. Find the equation of a line through the vertex B and the point P in AC; such that AP : CP = 2 : 3.
L is a point on the line segment PQ dividing it in the ratio 1 : 3. If the coordinates of P and Q are (3, 7) and ( 11,-5) respectively, find if L lies on the line 2x + 5y = 20.
Find the equation of a line with slope 1 and cutting off an intercept of 5 units on Y-axis.
In the adjoining figure, write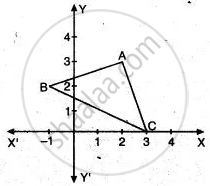
(i) The coordinates of A, B and C.
(ii) The equation of the line through A and | | to BC.
