Advertisements
Advertisements
Question
Find the value(s) of k so that PQ will be parallel to RS. Given : P(2, 4), Q(3, 6), R(8, 1) and S(10, k)
Solution
Since, PQ || RS,
Slope of PQ = Slope of RS
Slope of PQ = `(6 - 4)/(3 - 2) = 2`
Slope of RS = `(k - 1)/(10 - 8) = (k - 1)/2`
∴ `2 = (k - 1)/2`
k – 1 = 4
k = 5
APPEARS IN
RELATED QUESTIONS
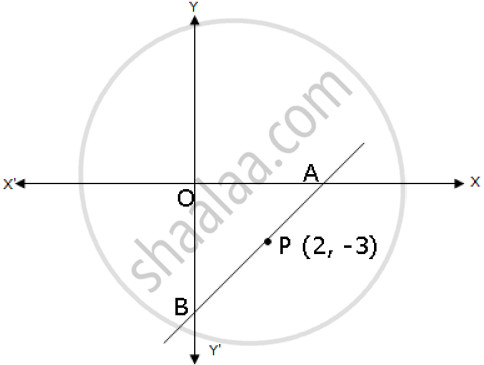
A and B are two points on the x-axis and y-axis respectively. P (2, −3) is the midpoint of AB. Find the:
(1) coordinates of A and B
(2) slope of line AB.
(3) an equation of line AB.
The points (K, 3), (2, −4) and (−K + 1, −2) are collinear. Find K.
Find the value of k for which the lines kx – 5y + 4 = 0 and 5x – 2y + 5 = 0 are perpendicular to each other.
Determine whether the following point is collinear.
R(1, –4), S(–2, 2), T(–3, 4)
Show that A(4, –1), B(6, 0), C(7, –2) and D(5, –3) are vertices of a square.
Find the slope of a line passing through the given pair of points (3,7) and (5,13)
Find the slope of a line parallel to the given line x +3y = 7
Find the slope of a line passing through the point A (-2,1), B (0,3).
Find the value of x so that the line passing through (3, 4) and (x, 5) makes an angle 135° with positive direction of X-axis.
Find the value, of k, if the line represented by kx – 5y + 4 = 0 and 4x – 2y + 5 = 0 are perpendicular to each other.
