Advertisements
Advertisements
Question
Lines mx + 3y + 7 = 0 and 5x – ny – 3 = 0 are perpendicular to each other. Find the relation connecting m and n.
Solution
mx + 3y + 7 = 0
3y = – mx − 7
`y = (-mx)/3 - 7/3`
Slope of this line = `(-m)/3`
5x − ny − 3 = 0
ny = 5x − 3
`y = (5x)/n - 3/n`
Slope of this line = `5/n`
Since, the lines are perpendicular; the product of their slopes is −1.
∴ `((-m)/3)(5/n) = -1`
5m = 3n
APPEARS IN
RELATED QUESTIONS
Find the slope of the line passing through the points A(-2, 1) and B(0, 3).
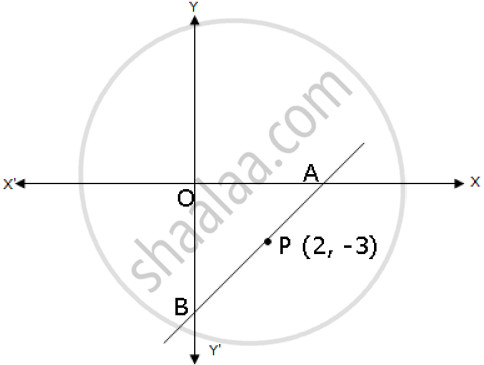
A and B are two points on the x-axis and y-axis respectively. P (2, −3) is the midpoint of AB. Find the:
(1) coordinates of A and B
(2) slope of line AB.
(3) an equation of line AB.
The side AB of an equilateral triangle ABC is parallel to the x-axis. Find the slopes of all its sides.

Find the slope and the inclination of the line AB if : A = `(-1, 2sqrt(3))` and B = `(-2, sqrt(3))`
Find the slope of the lines passing through the given point.
E(–4, –2) , F (6, 3)
Determine whether the following point is collinear.
P(2, –5), Q(1, –3), R(–2, 3)
Find the slope of a line passing through the given pair of points (9,-2) and (-5,5)
Find the slope of a line passing through the given pair of points (0,5) and (5,0)
Find the slope and the y-intercept of the following line 4y = 5x - 8
