Advertisements
Advertisements
Question
AB is a diameter of a circle with centre 0. If the ooordinates of A and 0 are ( 1, 4) and (3, 6 ). Find the ooordinates of B and the length of the diameter.
Solution

O is the centre of the circle with diameter AB .
∴ AO : OB = 1 : 1
Coordinnates of O are ,
O (3 , 6) = O `((1 + "x")/2 , (4 + "y")/2)`
`3 = (1 + "x")/2 , 6 = (4 + "y")/2`
6 = 1 + x , 12 = 4 + y
x = 5 , y = 8
Coordinates of B are (5 , 8)
Length of AB = `sqrt ((5 - 1)^2 + (8 - 4)^2)`
`= sqrt (16 + 16) = 4 sqrt 2` units
APPEARS IN
RELATED QUESTIONS
Prove that the points A(–5, 4); B(–1, –2) and C(5, 2) are the vertices of an isosceles right-angled triangle. Find the co-ordinates of D so that ABCD is a square.
Write the co-ordinates of the point of intersection of graphs of
equations x = 2 and y = -3.
(4, 2) and (-1, 5) are the adjacent vertices ofa parallelogram. (-3, 2) are the coordinates of the points of intersection of its diagonals. Find the coordinates of the other two vertices.
Three consecutive vertices of a parallelogram ABCD are A(S, 5), B(-7, -5) and C(-5, 5). Find the coordinates of the fourth vertex D.
If (-3, 2), (1, -2) and (5, 6) are the midpoints of the sides of a triangle, find the coordinates of the vertices of the triangle.
The centre ‘O’ of a circle has the coordinates (4, 5) and one point on the circumference is (8, 10). Find the coordinates of the other end of the diameter of the circle through this point.
Find the mid-point of the line segment joining the points
(−2, 3) and (−6, −5)
In what ratio does the point Q(1, 6) divide the line segment joining the points P(2, 7) and R(−2, 3)
Point P is the centre of the circle and AB is a diameter. Find the coordinates of points B if coordinates of point A and P are (2, – 3) and (– 2, 0) respectively.
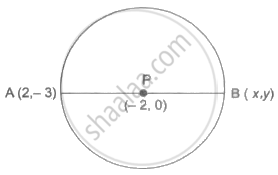
Given: A`square` and P`square`. Let B (x, y)
The centre of the circle is the midpoint of the diameter.
∴ Mid point formula,
`square = (square + x)/square`
⇒ `square = square` + x
⇒ x = `square - square`
⇒ x = – 6
and `square = (square + y)/2`
⇒ `square` + y = 0
⇒ y = 3
Hence coordinates of B is (– 6, 3).
ABC is a triangle whose vertices are A(1, –1), B(0, 4) and C(– 6, 4). D is the midpoint of BC. Find the coordinates of D.
