Advertisements
Advertisements
Question
Point P is the centre of the circle and AB is a diameter. Find the coordinates of points B if coordinates of point A and P are (2, – 3) and (– 2, 0) respectively.
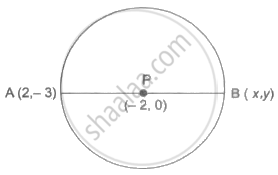
Given: A`square` and P`square`. Let B (x, y)
The centre of the circle is the midpoint of the diameter.
∴ Mid point formula,
`square = (square + x)/square`
⇒ `square = square` + x
⇒ x = `square - square`
⇒ x = – 6
and `square = (square + y)/2`
⇒ `square` + y = 0
⇒ y = 3
Hence coordinates of B is (– 6, 3).
Solution
Given: A(2, –3) and P(–2, 0). Let B (x, y)
The centre of the circle is the midpoint of the diameter.
∴ Mid point formula,
– 2 = `(bb2 + x)/bb2`
⇒ – 4 = 2 + x
⇒ x = – 4 – 2
⇒ x = – 6
and 0 = `(bb(-3) + y)/2`
⇒ – 3 + y = 0
⇒ y = 3
Hence coordinates of B is (– 6, 3).
APPEARS IN
RELATED QUESTIONS
ABCD is a parallelogram where A(x, y), B(5, 8), C(4, 7) and D(2, -4). Find
1) Coordinates of A
2) An equation of diagonal BD
Points A(–5, x), B(y, 7) and C(1, –3) are collinear (i.e. lie on the same straight line) such that AB = BC. Calculate the values of x and y.
The co-ordinates of the centroid of a triangle PQR are (2, –5). If Q = (–6, 5) and R = (11, 8); calculate the co-ordinates of vertex P.
In the following example find the co-ordinate of point A which divides segment PQ in the ratio a : b.
P(–3, 7), Q(1, –4), a : b = 2 : 1
Point P is the midpoint of seg AB. If co-ordinates of A and B are (-4, 2) and (6, 2) respectively then find the co-ordinates of point P.
(A) (-1,2) (B) (1,2) (C) (1,-2) (D) (-1,-2)
A(6, -2), B(3, -2) and C(S, 6) are the three vertices of a parallelogram ABCD. Find the coordinates of the fourth vertex c.
P( -2, 5), Q(3, 6 ), R( -4, 3) and S(-9, 2) are the vertices of a quadrilateral. Find the coordinates of the midpoints of the diagonals PR and QS. Give a special name to the quadrilateral.
Find the length of the median through the vertex A of triangle ABC whose vertices are A (7, -3), B(S, 3) and C(3, -1).
Two vertices of a triangle are ( -1, 4) and (5, 2). If the centroid is (0, 3), find the third vertex.
The midpoints of three sides of a triangle are (1, 2), (2, -3) and (3, 4). Find the centroid of the triangle.
P , Q and R are collinear points such that PQ = QR . IF the coordinates of P , Q and R are (-5 , x) , (y , 7) , (1 , -3) respectively, find the values of x and y.
AB is a diameter of a circle with centre 0. If the ooordinates of A and 0 are ( 1, 4) and (3, 6 ). Find the ooordinates of B and the length of the diameter.
Find the mid-point of the line segment joining the points
(8, −2) and (−8, 0)
Find the mid-point of the line segment joining the points
(a, b) and (a + 2b, 2a – b)
The coordinates of the point C dividing the line segment joining the points P(2, 4) and Q(5, 7) internally in the ratio 2 : 1 is
The ratio in which the x-axis divides the line segment joining the points A (a1, b1) and B (a2, b2) is
Find coordinates of midpoint of segment joining (– 2, 6) and (8, 2)
From the figure given alongside, find the length of the median AD of triangle ABC. Complete the activity.
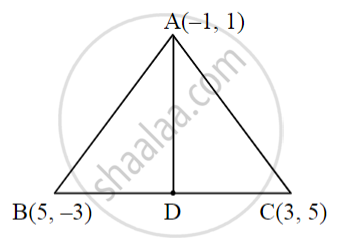
Solution:
Here A(–1, 1), B(5, – 3), C(3, 5) and suppose D(x, y) are coordinates of point D.
Using midpoint formula,
x = `(5 + 3)/2`
∴ x = `square`
y = `(-3 + 5)/2`
∴ y = `square`
Using distance formula,
∴ AD = `sqrt((4 - square)^2 + (1 - 1)^2`
∴ AD = `sqrt((square)^2 + (0)^2`
∴ AD = `sqrt(square)`
∴ The length of median AD = `square`
