Advertisements
Advertisements
Question
The co-ordinates of the centroid of a triangle PQR are (2, –5). If Q = (–6, 5) and R = (11, 8); calculate the co-ordinates of vertex P.
Solution
Let co-ordinates of P be (x, y)
And of centroid G are (2, –5)
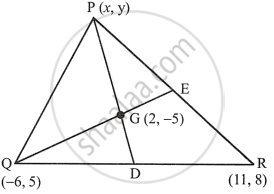
∴ `2 = (x_1 + x_2 + x_3)/3`
= `(x - 6 + 11)/3`
= `(x + 5)/3`
`=>` x + 5 = 6
∴ x = 6 – 5 = 1
And `-5 = (y_1 + y_2 + y_3)/3`
= `(y + 5 + 8)/3`
= `(y + 13)/3`
`=>` y + 13 = –15
∴ y = –15 – 13
= –28
Hence, co-ordinates of vertex P are (1, –28)
APPEARS IN
RELATED QUESTIONS
Find the mid-point of the line segment joining the points:
(–6, 7) and (3, 5)
Given M is the mid-point of AB, find the co-ordinates of B; if A = (3, –1) and M = (–1, 3).
M is the mid-point of the line segment joining the points A(–3, 7) and B(9, –1). Find the coordinates of point M. Further, if R(2, 2) divides the line segment joining M and the origin in the ratio p : q, find the ratio p : q.
Find the coordinates of the midpoint of the line segment joining P(0, 6) and Q(12, 20).
Point P is the midpoint of seg AB. If co-ordinates of A and B are (-4, 2) and (6, 2) respectively then find the co-ordinates of point P.
(A) (-1,2) (B) (1,2) (C) (1,-2) (D) (-1,-2)
A( 4, 2), B(-2, -6) and C(l, 1) are the vertices of triangle ABC. Find its centroid and the length of the median through C.
A(−3, 2), B(3, 2) and C(−3, −2) are the vertices of the right triangle, right angled at A. Show that the mid-point of the hypotenuse is equidistant from the vertices
The ratio in which the x-axis divides the line segment joining the points A (a1, b1) and B (a2, b2) is
In what ratio does the y-axis divides the line joining the points (−5, 1) and (2, 3) internally
Find coordinates of the midpoint of a segment joining point A(–1, 1) and point B(5, –7)
Solution: Suppose A(x1, y1) and B(x2, y2)
x1 = –1, y1 = 1 and x2 = 5, y2 = –7
Using midpoint formula,
∴ Coordinates of midpoint of segment AB
= `((x_1 + x_2)/2, (y_1+ y_2)/2)`
= `(square/2, square/2)`
∴ Coordinates of the midpoint = `(4/2, square/2)`
∴ Coordinates of the midpoint = `(2, square)`
