Advertisements
Advertisements
Question
A( 4, 2), B(-2, -6) and C(l, 1) are the vertices of triangle ABC. Find its centroid and the length of the median through C.
Solution
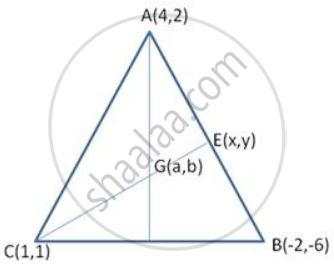
Let G (a,b) be at centroid of Δ ABC ,
Coordinates of G are ,
G (a , b) = G = `((4 - 2 +1)/3 , (2 - 6 + 1)/3)` = G (1 , -1)
Let CE be the median through C
∴ AE : EB = 1 : 1
Coordinates of E are
E (x , y) = E `((4 - 2)/2 , (2 - 6)/2)` = E (1 , -2)
Length of median CE = `sqrt ((1 - 1)^2 + (2 - 1)^2)`
`= sqrt 9`
= 3 units
APPEARS IN
RELATED QUESTIONS
P(4, 2) and Q(–1, 5) are the vertices of parallelogram PQRS and (–3, 2) are the co-ordinates of the point of intersection of its diagonals. Find co-ordinates of R and S.
Find the midpoint of the line segment joining the following pair of point :
( -3, 5) and (9, -9)
Two vertices of a triangle are (1, 4) and (3, 1). If the centroid of the triangle is the origin, find the third vertex.
The mid-point of the line segment joining A (- 2 , 0) and B (x , y) is P (6 , 3). Find the coordinates of B.
The coordinates of the centroid I of triangle PQR are (2, 5). If Q = (-6, 5) and R = (7, 8). Calculate the coordinates of vertex P.
Two vertices of a triangle are ( -1, 4) and (5, 2). If the centroid is (0, 3), find the third vertex.
P , Q and R are collinear points such that PQ = QR . IF the coordinates of P , Q and R are (-5 , x) , (y , 7) , (1 , -3) respectively, find the values of x and y.
Find the mid-point of the line segment joining the points
(−2, 3) and (−6, −5)
If the mid-point (x, y) of the line joining (3, 4) and (p, 7) lies on 2x + 2y + 1 = 0, then what will be the value of p?
From the figure given alongside, find the length of the median AD of triangle ABC. Complete the activity.
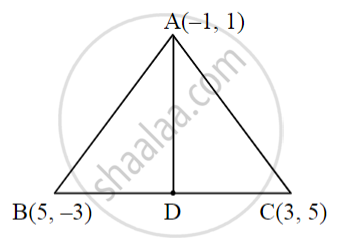
Solution:
Here A(–1, 1), B(5, – 3), C(3, 5) and suppose D(x, y) are coordinates of point D.
Using midpoint formula,
x = `(5 + 3)/2`
∴ x = `square`
y = `(-3 + 5)/2`
∴ y = `square`
Using distance formula,
∴ AD = `sqrt((4 - square)^2 + (1 - 1)^2`
∴ AD = `sqrt((square)^2 + (0)^2`
∴ AD = `sqrt(square)`
∴ The length of median AD = `square`
