Question

The coordinates of the centroid I of triangle PQR are (2, 5). If Q = (-6, 5) and R = (7, 8). Calculate the coordinates of vertex P. 

Answer 1

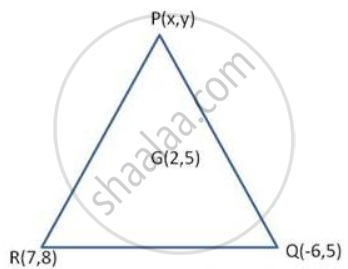
Let G be the centroid of Δ PQR whose coordinates are (2 , 5) and let (x , y) be the coordinates of vertex P.

Coordinates of G are ,

G (2 , 5) = G `(("x" - 6 + 7)/3 , ("y" + 5 + 8)/3)`

`2 = ("x" + 1)/3 , 5 = ("y" + 13)/3`

6 = x + 1  , 15 = y + 13

x = 5  , y =2

coordinates of vertex P are (5 , 2)