Advertisements
Advertisements
Question
A(6, -2), B(3, -2) and C(S, 6) are the three vertices of a parallelogram ABCD. Find the coordinates of the fourth vertex c.
Solution
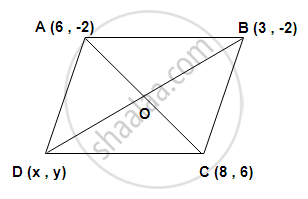
We know that in a parallelogram, diagonals bisect each other .
∴ midpoint of AC = midpoint of BD
`"O" ((6 + 8)/2 , (-2 + 6)/2) = "O" (("x" + 3)/2 , ("y" - 2)/2)`
`therefore (6 + 8)/2 = ("x" + 3)/2 , (-2 + 6)/2 = ("y" - 2)/2`
14 = x + 3 , 4 = y - 2
x = 11 , y = 6
the coordinates of the fourth vertex Dare ( 11,6)
APPEARS IN
RELATED QUESTIONS
Points A and B have co-ordinates (3, 5) and (x, y) respectively. The mid-point of AB is (2, 3). Find the values of x and y.
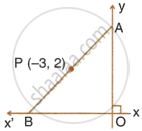
P(–3, 2) is the mid-point of line segment AB as shown in the given figure. Find the co-ordinates of points A and B.
(–5, 2), (3, −6) and (7, 4) are the vertices of a triangle. Find the length of its median through the vertex (3, −6).
A(–1, 0), B(1, 3) and D(3, 5) are the vertices of a parallelogram ABCD. Find the co-ordinates of vertex C.
Find the coordinates of point P if P divides the line segment joining the points A(–1, 7) and B(4, –3) in the ratio 2 : 3.
The coordinates of the end points of the diameter of a circle are (3, 1) and (7, 11). Find the coordinates of the centre of the circle.
Find the mid-point of the line segment joining the points
(−2, 3) and (−6, −5)
The centre of a circle is (−4, 2). If one end of the diameter of the circle is (−3, 7) then find the other end
The points A(−5, 4), B(−1, −2) and C(5, 2) are the vertices of an isosceles right-angled triangle where the right angle is at B. Find the coordinates of D so that ABCD is a square
Find the coordinates of point P where P is the midpoint of a line segment AB with A(–4, 2) and B(6, 2).
Solution :

Suppose, (–4, 2) = (x1, y1) and (6, 2) = (x2, y2) and co-ordinates of P are (x, y).
∴ According to the midpoint theorem,
x = `(x_1 + x_2)/2 = (square + 6)/2 = square/2 = square`
y = `(y_1 + y_2)/2 = (2 + square)/2 = 4/2 = square`
∴ Co-ordinates of midpoint P are `square`.
