Advertisements
Advertisements
Question
A triangle is formed by line segments joining the points (5, 1 ), (3, 4) and (1, 1). Find the coordinates of the centroid.
Solution
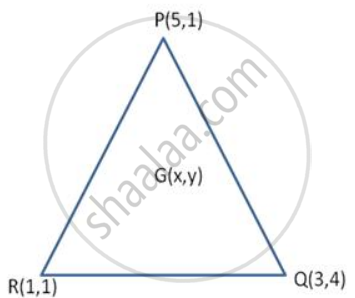
Let G (x , y) be he centroid of Δ PQR
Coordinates of G are ,
G (x , y) = G`((5 + 3 +1)/3 , (1 + 4 + 1)/3)`
= G (3 , 2)
APPEARS IN
RELATED QUESTIONS
Points P(a, −4), Q(−2, b) and R(0, 2) are collinear. If Q lies between P and R, such that PR = 2QR, calculate the values of a and b.
Point P is the centre of the circle and AB is a diameter . Find the coordinates of point B if coordinates of point A and P are (2, –3) and (–2, 0) respectively.
Find the midpoint of the line segment joining the following pair of point :
(a+b, b-a) and (a-b, a+b)
If the midpoints of the sides ofa triangle are (-2, 3), (4, -3), (4, 5), find its vertices.
Two vertices of a triangle are (1, 4) and (3, 1). If the centroid of the triangle is the origin, find the third vertex.
The centre ‘O’ of a circle has the coordinates (4, 5) and one point on the circumference is (8, 10). Find the coordinates of the other end of the diameter of the circle through this point.
If the mid-point (x, y) of the line joining (3, 4) and (p, 7) lies on 2x + 2y + 1 = 0, then what will be the value of p?
If the coordinates of one end of a diameter of a circle is (3, 4) and the coordinates of its centre is (−3, 2), then the coordinate of the other end of the diameter is
The ratio in which the x-axis divides the line segment joining the points A (a1, b1) and B (a2, b2) is
Find coordinates of midpoint of the segment joining points (0, 2) and (12, 14)
