Advertisements
Advertisements
Question
If the mid-point (x, y) of the line joining (3, 4) and (p, 7) lies on 2x + 2y + 1 = 0, then what will be the value of p?
Solution
Mid−point of a line = `((x_1 + x_2)/2, (y_1 + y_2)/2)`
(x, y) = `((3 + "p")/2, (4 + 7)/2)`
= `((3 + "p")/2, 11/2)`
The point `((3 + "p")/2, 11/2)` lies on 2x + 2y + 1 = 0
`2((3 + "p")/2) + 2 11/2 + 1` = 0
3 + p + 11 + 1 = 0
⇒ p + 15 = 0
⇒ p = −15
The value of p is −15.
APPEARS IN
RELATED QUESTIONS
Given M is the mid-point of AB, find the co-ordinates of A; if M = (1, 7) and B = (–5, 10).
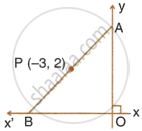
P(–3, 2) is the mid-point of line segment AB as shown in the given figure. Find the co-ordinates of points A and B.
A(6, -2), B(3, -2) and C(S, 6) are the three vertices of a parallelogram ABCD. Find the coordinates of the fourth vertex c.
A triangle is formed by line segments joining the points (5, 1 ), (3, 4) and (1, 1). Find the coordinates of the centroid.
Two vertices of a triangle are ( -1, 4) and (5, 2). If the centroid is (0, 3), find the third vertex.
The midpoints of three sides of a triangle are (1, 2), (2, -3) and (3, 4). Find the centroid of the triangle.
The centre of a circle is (a+2, a-1). Find the value of a, given that the circle passes through the points (2, -2) and (8, -2).
P , Q and R are collinear points such that PQ = QR . IF the coordinates of P , Q and R are (-5 , x) , (y , 7) , (1 , -3) respectively, find the values of x and y.
The three vertices of a parallelogram taken in order are (-1, 0), (3, 1) and (2, 2) respectively. Find the coordinates of the fourth vertex.
If (1, −2), (3, 6), (x, 10) and (3, 2) are the vertices of the parallelogram taken in order, then the value of x is
