Advertisements
Advertisements
Question
If (1, −2), (3, 6), (x, 10) and (3, 2) are the vertices of the parallelogram taken in order, then the value of x is
Options
6
5
4
3
Solution
5
Explanation;
Hint:
Since ABCD is a parallelogram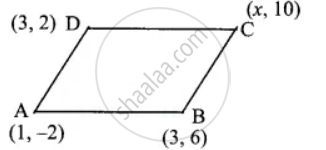
Mid-point of AC = Mid-point of BD
`((1 + x)/2, (-2 + 10)/2) = ((3 + 3)/2, (6 + 2)/2)`
`(1 + x)/2 = 6/2`
⇒ 1 + x = 6
⇒ x = 6 – 1 = 5
The value of x = 5
APPEARS IN
RELATED QUESTIONS
P(4, 2) and Q(–1, 5) are the vertices of parallelogram PQRS and (–3, 2) are the co-ordinates of the point of intersection of its diagonals. Find co-ordinates of R and S.
The centre of a circle is (a+2, a-1). Find the value of a, given that the circle passes through the points (2, -2) and (8, -2).
Let A(-a, 0), B(0, a) and C(α , β) be the vertices of the L1 ABC and G be its centroid . Prove that
GA2 + GB2 + GC2 = `1/3` (AB2 + BC2 + CA2)
A , B and C are collinear points such that AB = `1/2` AC . If the coordinates of A, B and C are (-4 , -4) , (-2 , b) anf (a , 2),Find the values of a and b.
AB is a diameter of a circle with centre 0. If the ooordinates of A and 0 are ( 1, 4) and (3, 6 ). Find the ooordinates of B and the length of the diameter.
A(3, 1), B(y, 4) and C(1, x) are vertices of a triangle ABC. P, Q and R are mid - points of sides BC, CA and AB respectively. Show that the centroid of ΔPQR is the same as the centroid ΔABC.
Find coordinates of midpoint of segment joining (– 2, 6) and (8, 2)
Find coordinates of the midpoint of a segment joining point A(–1, 1) and point B(5, –7)
Solution: Suppose A(x1, y1) and B(x2, y2)
x1 = –1, y1 = 1 and x2 = 5, y2 = –7
Using midpoint formula,
∴ Coordinates of midpoint of segment AB
= `((x_1 + x_2)/2, (y_1+ y_2)/2)`
= `(square/2, square/2)`
∴ Coordinates of the midpoint = `(4/2, square/2)`
∴ Coordinates of the midpoint = `(2, square)`
Find the coordinates of midpoint of segment joining (22, 20) and (0, 16)
If A(5, 4), B(–3, –2) and C(1, –8) are the vertices of a ∆ABC. Segment AD is median. Find the length of seg AD:
