Advertisements
Advertisements
Question
Calculate the co-ordinates of the centroid of the triangle ABC, if A = (7, –2), B = (0, 1) and C =(–1, 4).
Solution
Co-ordinates of the centroid of triangle ABC are
`((7 + 0 - 1)/3, (-2 + 1 + 4)/3)`
= `(6/3, 3/3)`
= (2, 1)
APPEARS IN
RELATED QUESTIONS
Points A(–5, x), B(y, 7) and C(1, –3) are collinear (i.e. lie on the same straight line) such that AB = BC. Calculate the values of x and y.
In the following example find the co-ordinate of point A which divides segment PQ in the ratio a : b.
P(–3, 7), Q(1, –4), a : b = 2 : 1
Point P is the centre of the circle and AB is a diameter . Find the coordinates of point B if coordinates of point A and P are (2, –3) and (–2, 0) respectively.
Find th co-ordinates of the midpoint of the line segment joining P(0, 6) and Q(12, 20).
If the midpoints of the sides ofa triangle are (-2, 3), (4, -3), (4, 5), find its vertices.
A lies on the x - axis amd B lies on the y -axis . The midpoint of the line segment AB is (4 , -3). Find the coordinates of A and B .
AB is a diameter of a circle with centre 0. If the ooordinates of A and 0 are ( 1, 4) and (3, 6 ). Find the ooordinates of B and the length of the diameter.
O(0, 0) is the centre of a circle whose one chord is AB, where the points A and B are (8, 6) and (10, 0) respectively. OD is the perpendicular from the centre to the chord AB. Find the coordinates of the mid-point of OD.
Point P is midpoint of segment AB where A(– 4, 2) and B(6, 2), then the coordinates of P are ______
From the figure given alongside, find the length of the median AD of triangle ABC. Complete the activity.
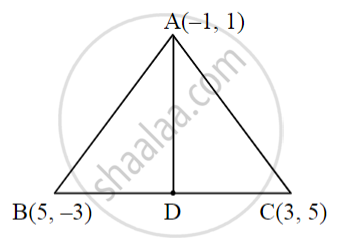
Solution:
Here A(–1, 1), B(5, – 3), C(3, 5) and suppose D(x, y) are coordinates of point D.
Using midpoint formula,
x = `(5 + 3)/2`
∴ x = `square`
y = `(-3 + 5)/2`
∴ y = `square`
Using distance formula,
∴ AD = `sqrt((4 - square)^2 + (1 - 1)^2`
∴ AD = `sqrt((square)^2 + (0)^2`
∴ AD = `sqrt(square)`
∴ The length of median AD = `square`
