Selina solutions for Mathematics [English] Class 10 ICSE chapter 13 - Section and Mid-Point Formula [Latest edition]

Calculate the co-ordinates of the point P which divides the line segment joining: A (1, 3) and B (5, 9) in the ratio 1 : 2

Calculate the co-ordinates of the point P which divides the line segment joining: A (–4, 6) and B (3, –5) in the ratio 3 : 2

In what ratio is the line joining (2, –3) and (5, 6) divided by the x-axis?

In what ratio is the line joining (2, –4) and (–3, 6) divided by the y-axis?

In what ratio does the point (1, a) divide the join of (–1, 4) and (4, –1)? Also, find the value of a.

In what ratio does the point (a, 6) divide the join of (–4, 3) and (2, 8)? Also, find the value of a.

In what ratio is the join of (4, 3) and (2, –6) divided by the x-axis? Also, find the co-ordinates of the point of intersection.

Find the ratio in which the join of (–4, 7) and (3, 0) is divided by the y-axis. Also, find the co-ordinates of the point of intersection.

Points A, B, C and D divide the line segment joining the point (5, –10) and the origin in five equal parts. Find the co-ordinates of B and D.

The line joining the points A (–3, –10) and B (–2, 6) is divided by the point P such that `(PB)/(AB) = 1/5`. Find the co-ordinates of P.

P is a point on the line joining A(4, 3) and B(–2, 6) such that 5AP = 2BP. Find the co-ordinates of P.

Calculate the ratio in which the line joining the points (–3, –1) and (5, 7) is divided by the line x = 2. Also, find the co-ordinates of the point of intersection.

Calculate the ratio in which the line joining A(6, 5) and B(4, –3) is divided by the line y = 2.

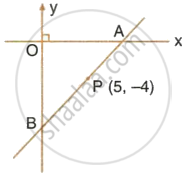
The point P (5, – 4) divides the line segment AB, as shown in the figure, in the ratio 2 : 5. Find the co-ordinates of points A and B. Given AP is smaller than BP.

Find the co-ordinates of the points of tri-section of the line joining the points (–3, 0) and (6, 6).

Show that the line segment joining the points (–5, 8) and (10, −4) is trisected by the co-ordinate axes.

Show that A (3, –2) is a point of trisection of the line segment joining the points (2, 1) and (5, −8). Also, find the co-ordinates of the other point of trisection.

If A = (−4, 3) and B = (8, −6)

1. Find the length of AB.
2. In what ratio is the line joining A and B, divided by the x-axis?

The line segment joining the points M(5, 7) and N(–3, 2) is intersected by the y-axis at point L. Write down the abscissa of L. Hence, find the ratio in which L divides MN. Also, find the co-ordinates of L.

A (2, 5), B (–1, 2) and C (5, 8) are the co-ordinates of the vertices of the triangle ABC. Points P and Q lie on AB and AC respectively, such that : AP : PB = AQ : QC = 1 : 2.

1. Calculate the co-ordinates of P and Q.
2. Show that : `PQ = 1/3 BC`.

A (–3, 4), B (3, –1) and C (–2, 4) are the vertices of a triangle ABC. Find the length of line segment AP, where point P lies inside BC, such that BP : PC = 2 : 3.

The line segment joining A (2, 3) and B (6, –5) is intercepted by x-axis at the point K. Write down the ordinate of the point K. Hence, find the ratio in which K divides AB. Also, find the coordinates of the point K.

The line segment joining A(4, 7) and B(−6, −2) is intercepted by the y – axis at the point K. write down the abscissa of the point K. hence, find the ratio in which K divides AB. Also, find the co-ordinates of the point K.

The line joining P(–4, 5) and Q(3, 2) intersects the y-axis at point R. PM and QN are perpendicular from P and Q on the x-axis Find:

1. the ratio PR : RQ
2. the coordinates of R.
3. the area of the quadrilateral PMNQ.

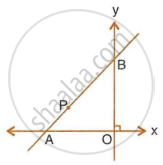
In the given figure, line APB meets the x-axis at point A and y-axis at point B. P is the point (−4, 2) and AP : PB = 1 : 2. Find the co-ordinates of A and B.

Given a line segment AB joining the points A(−4, 6) and B(8, −3). Find:

1. the ratio in which AB is divided by the y-axis.
2. find the coordinates of the point of intersection.
3. the length of AB.

If P(–b, 9a – 2) divides the line segment joining the points A(–3, 3a + 1) and B(5, 8a) in the ratio 3: 1, find the values of a and b.

Find the mid-point of the line segment joining the points:

(–6, 7) and (3, 5)

Find the mid-point of the line segment joining the points:

(5, –3) and (–1, 7)

Points A and B have co-ordinates (3, 5) and (x, y) respectively. The mid-point of AB is (2, 3). Find the values of x and y.

A(5, 3), B(–1, 1) and C(7, –3) are the vertices of triangle ABC. If L is the mid-point of AB and M is the mid-point of AC, show that : `LM = 1/2 BC`.

Given M is the mid-point of AB, find the co-ordinates of A; if M = (1, 7) and B = (–5, 10).

Given M is the mid-point of AB, find the co-ordinates of B; if A = (3, –1) and M = (–1, 3).

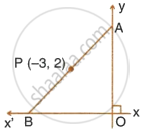
P(–3, 2) is the mid-point of line segment AB as shown in the given figure. Find the co-ordinates of points A and B.

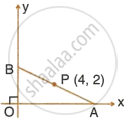
In the given figure, P(4, 2) is mid-point of line segment AB. Find the co-ordinates of A and B. 

(–5, 2), (3, −6) and (7, 4) are the vertices of a triangle. Find the length of its median through the vertex (3, −6).

Given a line ABCD in which AB = BC = CD, B = (0, 3) and C = (1, 8). Find the co-ordinates of A and D.

One end of the diameter of a circle is (–2, 5). Find the co-ordinates of the other end of it, if the centre of the circle is (2, –1).

A(2, 5), B(1, 0), C(−4, 3) and D(–3, 8) are the vertices of quadrilateral ABCD. Find the co-ordinates of the mid-points of AC and BD. Give a special name to the quadrilateral.

P(4, 2) and Q(–1, 5) are the vertices of parallelogram PQRS and (–3, 2) are the co-ordinates of the point of intersection of its diagonals. Find co-ordinates of R and S.

A(–1, 0), B(1, 3) and D(3, 5) are the vertices of a parallelogram ABCD. Find the co-ordinates of vertex C.

The points (2, –1), (–1, 4) and (–2, 2) are mid-points of the sides of a triangle. Find its vertices.

Points A(–5, x), B(y, 7) and C(1, –3) are collinear (i.e. lie on the same straight line) such that AB = BC. Calculate the values of x and y.

Points P(a, −4), Q(−2, b) and R(0, 2) are collinear. If Q lies between P and R, such that PR = 2QR, calculate the values of a and b.

Calculate the co-ordinates of the centroid of the triangle ABC, if A = (7, –2), B = (0, 1) and C =(–1, 4).

The co-ordinates of the centroid of a triangle PQR are (2, –5). If Q = (–6, 5) and R = (11, 8); calculate the co-ordinates of vertex P.

A(5, x), B(−4, 3) and C(y, –2) are the vertices of the triangle ABC whose centroid is the origin. Calculate the values of x and y.

Given a triangle ABC in which A = (4, −4), B = (0, 5) and C = (5, 10). A point P lies on BC such that BP : PC = 3 : 2. Find the length of line segment AP.

A(20, 0) and B(10, –20) are two fixed points. Find the co-ordinates of the point P in AB such that : 3PB = AB. Also, find the co-ordinates of some other point Q in AB such that : AB = 6 AQ.

A(–8, 0), B(0, 16) and C(0, 0) are the vertices of a triangle ABC. Point P lies on AB and Q lies on AC such that AP : PB = 3 : 5 and AQ : QC = 3 : 5. Show that : PQ = `3/8` BC.

Find the co-ordinates of points of trisection of the line segment joining the point (6, –9) and the origin.

A line segment joining A`(-1,5/3)` and B(a, 5) is divided in the ratio 1 : 3 at P, the point where the line segment AB intersects the y-axis.

1. Calculate the value of ‘a’.
2. Calculate the co-ordinates of ‘P’.

In what ratio is the line joining A(0, 3) and B(4, –1) divided by the x-axis? Write the co-ordinates of the point where AB intersects the x-axis.

The mid-point of the segment AB, as shown in diagram, is C(4, –3). Write down the co-ordinates of A and B.

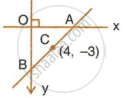
AB is a diameter of a circle with centre C = (–2, 5). If A = (3, –7), find

1. the length of radius AC.
2. the coordinates of B.

Find the co-ordinates of the centroid of a triangle ABC whose vertices are: A(–1, 3), B(1, –1) and C(5, 1).

The mid point of the line segment joining (4a, 2b – 3) and (−4, 3b) is (2, –2a). Find the values of a and b.

The mid-point of the line segment joining (2a, 4) and (–2, 2b) is (1, 2a + 1). Find the values of a and b.

1. Write down the co-ordinates of the point P that divides the line joining A(−4, 1) and B(17, 10) in the ratio 1 : 2.
2. Calculate the distance OP, where O is the origin.
3. In what ratio does the y-axis divide the line AB?

Prove that the points A(–5, 4); B(–1, –2) and C(5, 2) are the vertices of an isosceles right-angled triangle. Find the co-ordinates of D so that ABCD is a square.

M is the mid-point of the line segment joining the points A(–3, 7) and B(9, –1). Find the coordinates of point M. Further, if R(2, 2) divides the line segment joining M and the origin in the ratio p : q, find the ratio p : q.

Calculate the ratio in which the line joining A(-4,2) and B(3,6) is divided by point p(x,3). Also, find x 

Find the ratio in which the line 2x + y = 4 divides the line segment joining the point P(2, –2) and Q(3, 7).

If the abscissa of a point P is 2, find the ratio in which this point divides the line segment joining the point (−4, 3) and (6, 3). Also, find the co-ordinates of point P.

The line joining the points (2, 1) and (5, –8) is trisected at the point P and Q. If point P lies on the line 2x – y + k = 0, find the value of k. Also, find the co-ordinates of point Q.

Find the image of the point A(5, –3) under reflection in the point P(–1, 3).

M is the mid-point of the line segment joining the points A(0, 4) and B(6, 0). M also divides the line segment OP in the ratio 1 : 3. Find : 

1. co-ordinates of M
2. co-ordinates of P
3. length of BP

A(–4, 2), B(0, 2) and C(–2, –4) are vertices of a triangle ABC. P, Q and R are mid-points of sides BC, CA and AB respectively. Show that the centroid of ΔPQR is the same as the centroid of ΔABC.

A(3, 1), B(y, 4) and C(1, x) are vertices of a triangle ABC and G(3, 4) is its centroid. Find the values of x and y. Also, find the length of side BC.