Advertisements
Advertisements
Question
In what ratio is the line joining A(0, 3) and B(4, –1) divided by the x-axis? Write the co-ordinates of the point where AB intersects the x-axis.
Solution
Let the ratio be m1 : m2 when the x-axis intersects the line AB at P.
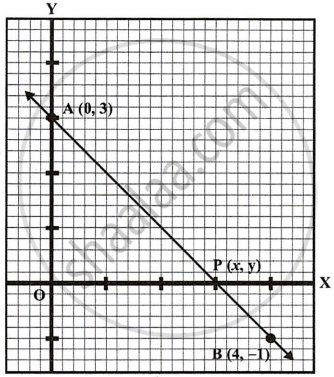
∴ Let co-ordinate of P(x, 0)
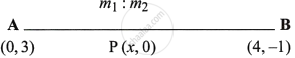
`x = (m_1x_2 + m_2x_1)/(m_1 + m_2), y = (m_1y_2 + m_2y_1)/(m_1 + m_2)`
`x = (m_1 xx 4 + m_2 xx 0)/(m_1 + m_2), y = (m_1(-1) + m_2 xx 3)/(m_1 + m_2)`
`x = (4m_1)/(m_1 + m_2), y = (-m_1 + 3m_2)/(m_1 + m_2)`
∵ P lies on x-axis,
∴ y = 0
∴ `(-m_1 + 3m_2)/(m_1 + m_2) = 0`
`=>` – m1 + 3m2 = 0
`=>` m1 = 3m2
`=> m_1/m_2 = 3/1`
`=>` m1 : m2 = 3 : 1
Now, `x = (4 xx 3)/(3 + 1)`
= `12/4`
= 3
∴ Required co-ordinates of P will be (3, 0)
APPEARS IN
RELATED QUESTIONS
Let P and Q be the points of trisection of the line segment joining the points A(2, -2) and B(-7, 4) such that P is nearer to A. Find the coordinates of P and Q.
If A (5, –1), B(–3, –2) and C(–1, 8) are the vertices of triangle ABC, find the length of median through A and the coordinates of the centroid.
Find the coordinates of the centroid of a triangle whose vertices are (–1, 0), (5, –2) and (8, 2)
Find the coordinates of the point which divides the join of (–1, 7) and (4, –3) in the ratio 2 : 3.
If (1, 2), (4, y), (x, 6) and (3, 5) are the vertices of a parallelogram taken in order, find x and y.
Find the ratio in which the join of (–4, 7) and (3, 0) is divided by the y-axis. Also, find the co-ordinates of the point of intersection.
The line joining the points A (–3, –10) and B (–2, 6) is divided by the point P such that `(PB)/(AB) = 1/5`. Find the co-ordinates of P.
If the coordinates of one end of a diameter of a circle are (2, 3) and the coordinates of its centre are (−2, 5), then the coordinates of the other end of the diameter are:
Find the ratio in which the point P (2, 4) divides the line joining points (-3, 1) and (7, 6).
If P(9a – 2, – b) divides line segment joining A(3a + 1, –3) and B(8a, 5) in the ratio 3 : 1, find the values of a and b.
