Advertisements
Advertisements
Question
The mid-point of the segment AB, as shown in diagram, is C(4, –3). Write down the co-ordinates of A and B.
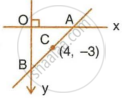
Solution
Since, point A lies on x-axis, let the co-ordinates of point A be (x, 0).
Since, point B lies on y-axis, let the co-ordinates of point B be (0, y).
Given, mid-point of AB is C(4, −3).
∴ `(4, -3) = ((x + 0)/2, (0 + y)/2)`
`=> (4 - 3) = (x/2, y/2)`
`=> 4 = x/2` and `-3 = y/2`
`=>` x = 8 and y = −6
Thus, the co-ordinates of point A are (8, 0) and the co-ordinates of point B are (0, −6).
APPEARS IN
RELATED QUESTIONS
Let P and Q be the points of trisection of the line segment joining the points A(2, -2) and B(-7, 4) such that P is nearer to A. Find the coordinates of P and Q.
Find the ratio in which y-axis divides the line segment joining the points A(5, –6) and B(–1, –4). Also find the coordinates of the point of division.
Find the coordinates of points which trisect the line segment joining (1, –2) and (–3, 4)
If the points A (6, 1), B (8, 2), C(9, 4) and D(p, 3) are vertices of a parallelogram, taken in order, find the value of p
If the coordinates of the mid-points of the sides of a triangle are (1, 2) (0, –1) and (2, 1). Find the coordinates of its vertices.
Find the coordinates of the centroid of a triangle whose vertices are (–1, 0), (5, –2) and (8, 2)
In what ratio does the point (a, 6) divide the join of (–4, 3) and (2, 8)? Also, find the value of a.
Points A, B, C and D divide the line segment joining the point (5, –10) and the origin in five equal parts. Find the co-ordinates of B and D.
The origin o (0, O), P (-6, 9) and Q (12, -3) are vertices of triangle OPQ. Point M divides OP in the ratio 1: 2 and point N divides OQ in the ratio 1: 2. Find the coordinates of points M and N. Also, show that 3MN = PQ.
If point P(1, 1) divide segment joining point A and point B(–1, –1) in the ratio 5 : 2, then the coordinates of A are ______
