Advertisements
Advertisements
Question
Find the coordinates of points which trisect the line segment joining (1, –2) and (–3, 4)
Sum
Solution
Let A(1, –2) and B(–3, 4) be the given points.
Let the points of trisection be P and Q. Then,
AP = PQ = QB = λ (say).
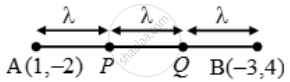
∴ PB = PQ + QB = 2λ and AQ = AP + PQ = 2λ
⇒ AP : PB = λ : 2λ = 1 : 2 and
AQ : QB = 2λ : λ = 2 : 1
So, P divides AB internally in the ratio 1 : 2 while Q divides internally in the ratio 2 : 1. Thus, the coordinates of P and Q are
`P( \frac{1\times (-3)+2\times 1}{1+2},\ \frac{1\times 4+2\times (-2)}{1+2})=P( \frac{-1}{3},\ 0)`
`Q( \frac{2\times (-3)+1\times 1}{2+1},\ \frac{2\times 4+1\times (-2)}{2+1})=Q( \frac{-5}{3},\ 2)" respectively"`
Hence, the two points of trisection are (–1/3, 0) and (–5/3, 2).
shaalaa.com
Is there an error in this question or solution?
