Question

Find the coordinates of points which trisect the line segment joining (1, –2) and (–3, 4)

Answer 1

Let A(1, –2) and B(–3, 4) be the given points.

Let the points of trisection be P and Q. Then,

AP = PQ = QB = λ (say).

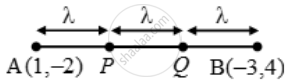
∴ PB = PQ + QB = 2λ and AQ = AP + PQ = 2λ

⇒ AP : PB = λ : 2λ = 1 : 2 and

AQ : QB = 2λ : λ = 2 : 1

So, P divides AB internally in the ratio 1 : 2 while Q divides internally in the ratio 2 : 1. Thus, the coordinates of P and Q are

`P( \frac{1\times (-3)+2\times 1}{1+2},\ \frac{1\times 4+2\times (-2)}{1+2})=P( \frac{-1}{3},\ 0)`

`Q( \frac{2\times (-3)+1\times 1}{2+1},\ \frac{2\times 4+1\times (-2)}{2+1})=Q( \frac{-5}{3},\ 2)" respectively"`

Hence, the two points of trisection are (–1/3, 0) and (–5/3, 2).