Advertisements
Advertisements
Question
Find the ratio in which the point P (2, 4) divides the line joining points (-3, 1) and (7, 6).
Solution
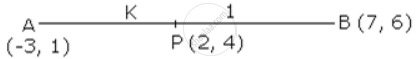
Let the point P divides AB in the ratio k : 1.
Coordinates of P are
x = `(7"k" - 3)/("k" + 1)`
y = `(6"k" + 1)/("k" + 1)`
But given, P(x, y) =P(2, 4)
`therefore 2 = (7"k" - 3)/("k" + 1)`
⇒ 2k + 2 = 7k - 3
⇒ 5 = 5k
⇒ k = 1
k : 1 = 1 : 1
or `4 = (6"k" + 1)/("k" + 1)`
4k + 4 = 6k + 1
⇒ 3 = 2k
⇒ k = `3/2`
k : 1=3 : 2
APPEARS IN
RELATED QUESTIONS
Find the coordinates of points which trisect the line segment joining (1, –2) and (–3, 4)
Determine the ratio in which the line 3x + y – 9 = 0 divides the segment joining the points (1, 3) and (2, 7)
If the points A (6, 1), B (8, 2), C (9, 4) and D (k, p) are the vertices of a parallelogram taken in order, then find the values of k and p.
In what ratio is the join of (4, 3) and (2, –6) divided by the x-axis? Also, find the co-ordinates of the point of intersection.
Calculate the ratio in which the line joining A(6, 5) and B(4, –3) is divided by the line y = 2.
Find the ratio in which the line x = O divides the join of ( -4, 7) and (3, 0).
Also, find the coordinates of the point of intersection.
Find the points of trisection of the segment joining A ( -3, 7) and B (3, -2).
A line intersects the y-axis and x-axis at the points P and Q respectively. If (2, -5) is the mid-point of PQ, then the coordinates of P and Q are respectively.
If (a/3, 4) is the mid-point of the segment joining the points P(-6, 5) and R(-2, 3), then the value of ‘a’ is ______.
Complete the following activity to find the coordinates of point P which divides seg AB in the ratio 3:1 where A(4, – 3) and B(8, 5).
Activity:
∴ By section formula,
∴ x = `("m"x_2 + "n"x_1)/square`,
∴ x = `(3 xx 8 + 1 xx 4)/(3 + 1)`,
= `(square + 4)/4`,
∴ x = `square`,
∴ y = `square/("m" + "n")`
∴ y = `(3 xx 5 + 1 xx (-3))/(3 + 1)`
= `(square - 3)/4`
∴ y = `square`
