Advertisements
Advertisements
Question
If the points A (6, 1), B (8, 2), C (9, 4) and D (k, p) are the vertices of a parallelogram taken in order, then find the values of k and p.
Solution
Let ABCD be a parallelogram in which the coordinates of the vertices are A (6, 1); B (8, 2); C (9, 4) and D (k, p).
Since ABCD is a parallelogram, the diagonals bisect each other. Therefore the mid-point of the diagonals of the parallelogram will coincide.
In general to find the mid-point P(x,y) of two points `A(x_1, y_1)` and `B(x_2,y_2)` we use section formula as,
`P(x,y) = ((x_1 + x_2)/2","(y_1 + y_2)/2)`
The mid-point of the diagonals of the parallelogram will coincide.
So,
Co-ordinate of mid-point o AC = Co-ordinate of mid-point of BD
Therefore,
`((6 + 9)/2, (4 + 1)/2) = ((k + 8)/2","(p + 2)/2))`
Now equate the individual terms to get the unknown value. So,
`(k + 8)/2 = 15/2`
k = 7
Similarly,
`(p + 2)/2 = 5/2`
p = 3
Therefore, k = 7 and p = 3
APPEARS IN
RELATED QUESTIONS
If A (5, –1), B(–3, –2) and C(–1, 8) are the vertices of triangle ABC, find the length of median through A and the coordinates of the centroid.
Find the ratio in which P(4, m) divides the line segment joining the points A(2, 3) and B(6, –3). Hence find m.
If A and B are two points having coordinates (−2, −2) and (2, −4) respectively, find the coordinates of P such that `AP = 3/7 AB`
Find the co-ordinates of the points of tri-section of the line joining the points (–3, 0) and (6, 6).
If A = (−4, 3) and B = (8, −6)
- Find the length of AB.
- In what ratio is the line joining A and B, divided by the x-axis?
The line segment joining A (2, 3) and B (6, –5) is intercepted by x-axis at the point K. Write down the ordinate of the point K. Hence, find the ratio in which K divides AB. Also, find the coordinates of the point K.
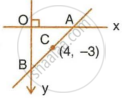
The mid-point of the segment AB, as shown in diagram, is C(4, –3). Write down the co-ordinates of A and B.
Find the ratio in which the line x = -2 divides the line segment joining (-6, -1) and (1, 6). Find the coordinates of the point of intersection.
The fourth vertex D of a parallelogram ABCD, whose three vertices are A(–2, 3), B(6, 7) and C(8, 3), is ______.
If A and B are (– 2, – 2) and (2, – 4) respectively; then find the co-ordinates of the point P such that `(AB)/(AB) = 3/7`.
