Advertisements
Advertisements
Question
If A and B are (– 2, – 2) and (2, – 4) respectively; then find the co-ordinates of the point P such that `(AB)/(AB) = 3/7`.
Solution
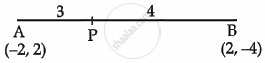
`(AP)/(AB) = 3/7`
∴ `(AP)/(PB) = 3/4`
`P((m_1x_2 + m_2x_1)/(m_1 + m_2), (m_1y_2 + m_2y_1)/(m_1 + m_2))`
= `(3 xx 2 + 4(-2))/(3 + 4), (3 xx -4 + 4 xx (2))/(3 + 4)`
= `((-2)/7, 4/7)`
APPEARS IN
RELATED QUESTIONS
The line segment joining the points (3, -4) and (1, 2) is trisected at the points P and Q. If the coordinates of P and Q are (p, -2) and (5/3, q) respectively. Find the values of p and q.
In what ratio does the point (a, 6) divide the join of (–4, 3) and (2, 8)? Also, find the value of a.
Calculate the ratio in which the line joining A(6, 5) and B(4, –3) is divided by the line y = 2.
Show that A (3, –2) is a point of trisection of the line segment joining the points (2, 1) and (5, −8). Also, find the co-ordinates of the other point of trisection.
A(20, 0) and B(10, –20) are two fixed points. Find the co-ordinates of the point P in AB such that : 3PB = AB. Also, find the co-ordinates of some other point Q in AB such that : AB = 6 AQ.
If the point C (–1, 2) divides internally the line-segment joining the points A (2, 5) and B (x, y) in the ratio 3 : 4, find the value of x2 + y2 ?
A (30, 20) and B ( 6, -4) are two fixed points. Find the coordinates of a point Pin AB such that 2PB = AP. Also, find the coordinates of some other point Qin AB such that AB = 6 AQ.
Find the ratio in which the point P (2, 4) divides the line joining points (-3, 1) and (7, 6).
Find the ratio In which is the segment joining the points (1, - 3} and (4, 5) ls divided by x-axis? Also, find the coordinates of this point on the x-axis.
The points A(x1, y1), B(x2, y2) and C(x3, y3) are the vertices of ∆ABC. What are the coordinates of the centroid of the triangle ABC?
