Advertisements
Advertisements
Question
A solid is in the shape of a cone standing on a hemisphere with both their diameters being equal to 1 cm and the height of the cone is equal to its radius. Find the volume of the solid. [Use π = 3.14]
Solution
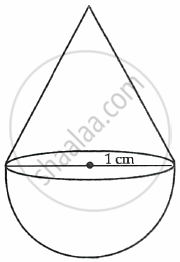
Diameter of cone (r) = Diameter of hemisphere (r)
Height of cone (h) = Radius of cone = `1/2`cm
Volume of the solid = Volume of the cone + Volume of the hemisphere
= `1/3 πr^2h + 2/3 πr^3`
= `(πr^2)/3 (h + 2r)`
= `π/3(1/2)^2 (1/2 + 2 xx 1/2)`
= `π/(3 xx 4) (3/2) cm^3`
= `3.14/8 cm^3`
∴ Volume of the solid = 0.3925 cm3
APPEARS IN
RELATED QUESTIONS
A cylindrical tube of radius 12cm contains water to a depth of 20cm. A spherical ball of radius 9cm is dropped into the tube and thus level of water is raised by hcm. What is the value of h.
The largest sphere is to be curved out of a right circular of radius 7cm and height 14cm. find volume of sphere?
A circus tent has cylindrical shape surmounted by a conical roof. The radius of the cylindrical base is 20 m. The heights of the cylindrical and conical portions are 4.2 m and 2.1 m respectively. Find the volume of the tent.
A cylindrical road roller made of iron is 1 m long, Its internal diameter is 54 cm and the thickness of the iron sheet used in making the roller is 9 cm. Find the mass of the roller, if 1 cm3 of iron has 7.8 gm mass. (Use π = 3.14)
If the volumes of two cones are in the ratio of 1:4 and their diameters are in the ratio of 4:5, then find the ratio of their heights.
The ratio between the radius of the base and the height of a cylinder is 2 : 3. If the volume of the cylinder is 12936 cm3, then find the radius of the base of the cylinder.
A cylinder with base radius 8 cm and height 2 cm is melted to form a cone of height 6 cm. Calculate the radius of the base of the cone.
The sum of the inner and the outer curved surfaces of a hollow metallic cylinder is 1056 cm2 and the volume of material in it is 1056 cm3. Find its internal and external radii. Given that the height of the cylinder is 21 cm.
Marbles of diameter 1.4 cm are dropped into a cylindrical beaker of diameter 7 cm containing some water. Find the number of marbles that should be dropped into the beaker so that the water level rises by 5.6 cm.
A solid right circular cone of height 120 cm and radius 60 cm is placed in a right circular cylinder full of water of height 180 cm such that it touches the bottom. Find the volume of water left in the cylinder, if the radius of the cylinder is equal to the radius of the cone.
