Advertisements
Advertisements
Question
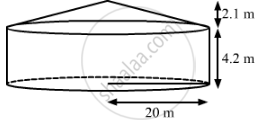
A circus tent has cylindrical shape surmounted by a conical roof. The radius of the cylindrical base is 20 m. The heights of the cylindrical and conical portions are 4.2 m and 2.1 m respectively. Find the volume of the tent.
Solution
Given that:
Radius of the cylindrical base r= 20 m
Height of the cylindrical portion h2 = 4.2 m
Height of the conical portion h2 = 2.1 m
The volume of the cylinder is given by the following formula
`V_1=pir^2h_1`
`=22/7xx20^2xx4.2`
The volume of the conical portion is
`V_2=1/3pir^2h_2`
`=1/3xx22/7xx20^2xx2.1`
= 880 m3
Therefore, the total volume of the circus tent is
V = V1 + V2
= 5280 + 880
= 6160 m3
Hence, the volume of the circus tent is V = 6160 m3
APPEARS IN
RELATED QUESTIONS
How many balls each of radius 1cm can be made from a solid sphere of lead of radius
8cm?
The difference between outside and inside surface areas of cylindrical metallic pipe 14 cm long is 44 m2. If the pipe is made of 99 cm3 of metal, find the outer and inner radii of the pipe.
If the volumes of two cones are in the ratio of 1:4 and their diameters are in the ratio of 4:5, then find the ratio of their heights.
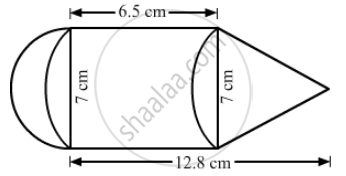
The adjoining figure represents a solid consisting of a cylinder surmounted by a cone at one end and a hemisphere at the other. Find the volume of the solid.
A solid right circular cone of height 60 cm and radius 30 cm is dropped in a right circular cylinder full of water, of height 180 cm and radius 60 cm. Find the volume of water left in the cylinder, in cubic metres.
A hemispherical bowl of internal diameter 30 cm is full of a liquid. This liquid is poured into cylindrical bottles of diameter 5 cm and height 6 cm each. How many bottles are required?
An iron pillar has some part in the form of a right circular cylinder and remaining in the form of a right circular cone. The radius of the base of each of cone and cylinder is 8 cm. The cylindrical part is 240 cm high and the conical part is 36 cm high. Find the weight of the pillar if one cubic cm of iron weight is 7.8 grams.
The radius of a wire is decreased to one third. If volume remains the same, the length will become ______.
A building is in the form of a cylinder surmounted by a hemispherical vaulted dome and contains `41 19/21 m^3` of air. If the internal diameter of dome is equal to its total height above the floor, find the height of the building?
The sum of the length, breadth and height of a cuboid is `6sqrt(3)` cm and the length of its diagonal is `2sqrt(3)` cm. The total surface area of the cuboid is ______.
